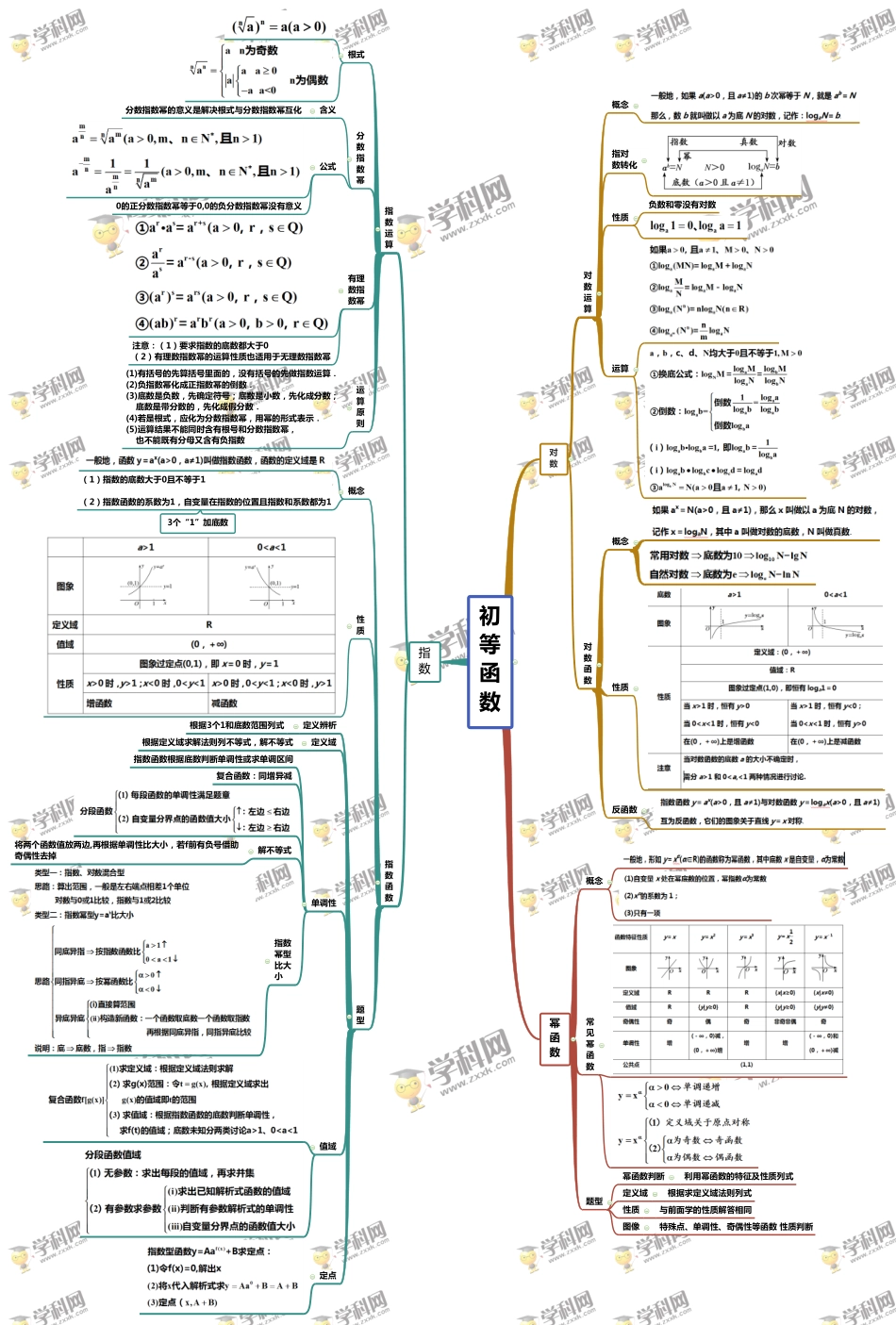
3个“1”加底数初等函数对数指数对数运算概念指对数转化性质运算负数和零没有对数对数函数概念性质反函数指数运算根式分数指数幂含义公式分数指数幂的意义是解决根式与分数指数幂互化0的正分数指数幂等于0,0的负分数指数幂没有意义有理数指数幂注意:(1)要求指数的底数都大于0(2)有理数指数幂的运算性质也适用于无理数指数幂运算原则(1)有括号的先算括号里面的,没有括号的先做指数运算.(2)负指数幂化成正指数幂的倒数.(3)底数是负数,先确定符号;底数是小数,先化成分数;底数是带分数的,先化成假分数.(4)若是根式,应化为分数指数幂,用幂的形式表示.(5)运算结果不能同时含有根号和分数指数幂,也不能既有分母又含有负指数幂函数概念常见幂函数题型幂函数判断定义域性质图像利用幂函数的特征及性质列式根据求定义域法则列式与前面学的性质解答相同特殊点、单调性、奇偶性等函数性质判断指数函数概念性质(1)指数的底数大于0且不等于1(2)指数函数的系数为1,自变量在指数的位置且指数和系数都为1题型定义辨析定义域单调性值域根据3个1和底数范围列式根据定义域求解法则列不等式,解不等式指数函数根据底数判断单调性或求单调区间复合函数:同增异减定点解不等式将两个函数值放两边,再根据单调性比大小,若f前有负号借助奇偶性去掉指数幂型比大小