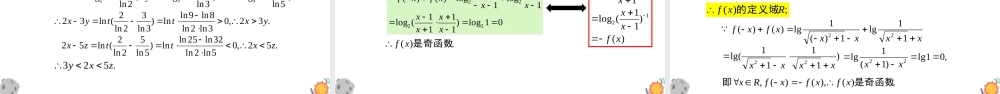4.4 对数函数(含3课时)-2022-2023学年高一数学教材配套教学精品课件（人教A版2019必修第一册).pptxVIP免费

4.4对数函数4.4.1对数函数的概念新知引入xayyxalog的函数是xy)10(logaaxya且母字换调与之对应都有唯一的在即yRx),0(,:与之对应都有唯一的Rxy),,0(,10aa且若的函数是yx一、对数函数的定义及性质)10(log:aaxya且对数函数._____)3(._______)2(______;,)1(定点为值域为定义域为是自变量xxay),0(R)0,1(01loga绘图索质二、对数型函数的定点._________4)23(log][恒过定点例xya440,1123yxx得令)4,1(01log},10|{aaaaa且._________)102(log22021]1[恒过定点变式xya._________112log]2[恒过定点变式xxeya2021022021,1011102yxx得令)2021,101(eeyxxx0,21112得令),2(e三、对数型函数的定义域}.0|{.0,02xxxx定义域为).4,(.4,04定义域为xx)1,()31,(01x031x00lgxx}10|{xxx且0x}0|{xx)82(log)5(23xxy0)2)(4(822xxxx),4()2,(三、对数型函数的定义域.][求下列函数的定义域变式)2lg()1(xy)6(log2)2(3xy)1ln(31)3(xxy).,1[,122,0)2lg(02定义域为xxxx].7,2(,292,)2(log2063定义域为xxxx解对数不等式：化同底+单调性).3,1(,13,0103定义域为xxxx322lg)4(xy).2,2(,02,02232定义域为xx)34(log][5.0xy变yaxxy2log对数函数),0(值域为定义域为RR值域为定义域为),0()(yaxxayx,y互换定义域和值域互换)1(logaxya)1(aayx互为反函数与指数函数对数函数xaayxylog四、反函数②存在反函数的条件是原函数必须“一一对应”.③若两函数互为反函数，则定义域和值域互换，且图象关于y=x对称.①对于y=f(x)，互换x,y得其反函数x=g(y))(yax互为反函数与指数函数对数函数xaayxylog四、反函数.______)1(,log)(]1[3xfxyxyxfy则对称的图象关于直线的图象与函数练习.______)22(,3)8()10()(]2[ffaaayxfyx则的反函数且且是函数练习13xxxf3)(xxfalog)(.21,8,38log)8(3aafa即232log22log)22(23212f4.4对数函数4.4.2对数函数的图象和性质一、对数函数的图象及性质)10(log:aaxya且对数函数:)4(._____)...