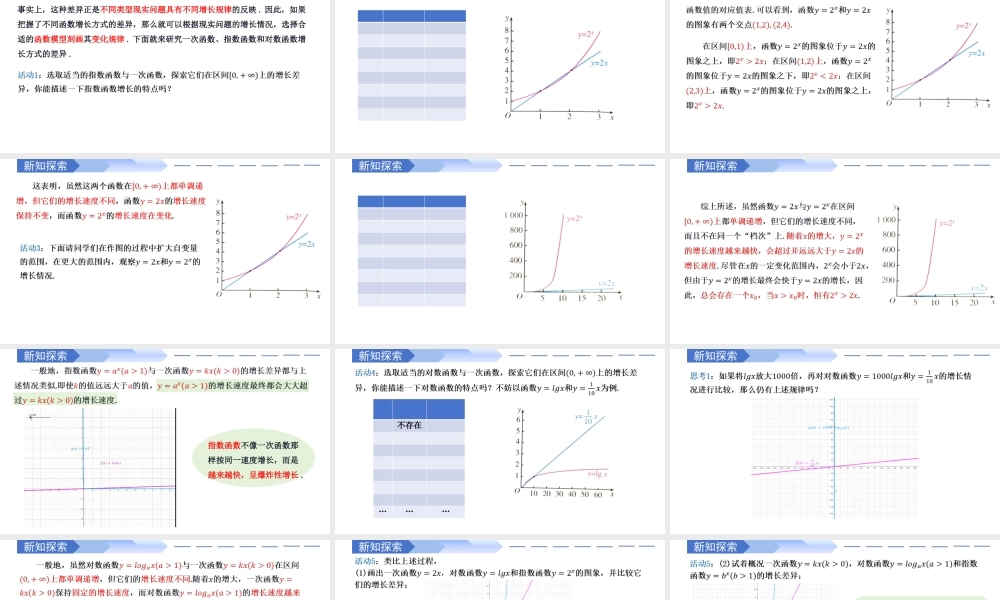
4.4对数函数4.4.3不同函数增长的差异第四章指数函数与对数函数复习引入在前面的学习中我们看到,一次函数与指数函数的增长方式存在很大差异.事实上,这种差异正是不同类型现实问题具有不同增长规律的反映.因此,如果把握了不同函数增长方式的差异,那么就可以根据现实问题的增长情况,选择合适的函数模型刻画其变化规律.下面就来研究一次函数、指数函数和对数函数增长方式的差异.新知探索新知探索新知探索新知探索新知探索新知探索指数函数不像一次函数那样按同一速度增长,而是越来越快,呈爆炸性增长.新知探索不存在………新知探索新知探索对数函数比较适合于描述增长速度平缓的变化规律.新知探索新知探索新知探索活动5:类比上述过程,(3)讨论交流“直线上升”“对数增长”“指数爆炸”的含义.练习题型一:三类函数模型增长差异的比较答案:A.一次函数、指数函数和对数函数三类函数模型中,指数增长最快.练习新知探索答案:A.根据已知所给的散点图,观察得到图象在第一象限,且从左到右图象是上升的,并且增长速度越来越快,根据四个选项中函数的增长趋势可知,用指数函数拟合最好,故选A.新知探索题型二:函数模型的选择练习方法技巧:几类不同增长函数模型选择的方法:(1)增长速度不变,即自变量增加相同量时,函数值的增量相等,此时的函数模型是一次函数模型.(2)增长速度越来越快,即自变量增加相同量时,函数值的增量成倍增加,此时的函数模型是指数函数模型.(3)增长速度越来越慢,即自变量增加相同量时,函数值的增量越来越小,此时的函数模型是对数函数模型.练习课堂小结&作业谢谢学习Thankyouforlearning