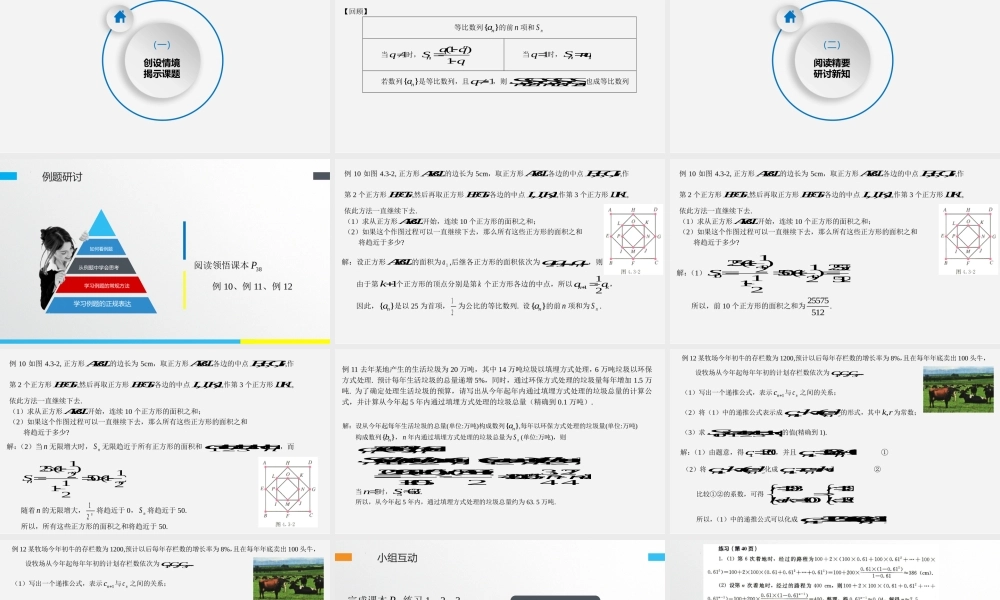
4.3.2.2等比数列的前n项和公式的应用第四章数列凯里一中尹洪January26,2025(一)创设情境揭示课题【回顾】等比数列{}na的前n项和nS当1q时,1(1)1nnaqSq当1q时,1nSna若数列{}na是等比数列,且1q,则232,,,...nnnnnSSSSS也成等比数列(二)阅读精要研讨新知例题研讨学习例题的正规表达学习例题的常规方法从例题中学会思考如何看例题阅读领悟课本38P例10、例11、例12例10如图4.3-2,正方形ABCD的边长为5cm,取正方形ABCD各边的中点,,,EFGH,作第2个正方形EFGH,然后再取正方形EFGH各边的中点,,,IJKL,作第3个正方形IJKL,依此方法一直继续下去.(1)求从正方形ABCD开始,连续10个正方形的面积之和;(2)如果这个作图过程可以一直继续下去,那么所有这些正方形的面积之和将趋近于多少?解:设正方形ABCD的面积为1a,后继各正方形的面积依次为23,,...,,...naaa,则由于第1k个正方形的顶点分别是第k个正方形各边的中点,所以112kkaa,因此,{}na是以25为首项,12为公比的等比数列.设{}na的前n项和为nS.例10如图4.3-2,正方形ABCD的边长为5cm,取正方形ABCD各边的中点,,,EFGH,作第2个正方形EFGH,然后再取正方形EFGH各边的中点,,,IJKL,作第3个正方形IJKL,依此方法一直继续下去.(1)求从正方形ABCD开始,连续10个正方形的面积之和;(2)如果这个作图过程可以一直继续下去,那么所有这些正方形的面积之和将趋近于多少?解:(1)101010125(1)125575250(1)1251212S所以,前10个正方形的面积之和为25575512.例10如图4.3-2,正方形ABCD的边长为5cm,取正方形ABCD各边的中点,,,EFGH,作第2个正方形EFGH,然后再取正方形EFGH各边的中点,,,IJKL,作第3个正方形IJKL,依此方法一直继续下去.(1)求从正方形ABCD开始,连续10个正方形的面积之和;(2)如果这个作图过程可以一直继续下去,那么所有这些正方形的面积之和将趋近于多少?解:(2)当n无限增大时,nS无限趋近于所有正方形的面积和123......naaaa,而125(1)1250(1)1212nnnS随着n的无限增大,12n将趋近于0,nS将趋近于50.所以,所有这些正方形的面积之和将趋近于50.例11去年某地产生的生活垃圾为20万吨,其中14万吨垃圾以填埋方式处理,6万吨垃圾以环保方式处理.预计每年生活垃圾的总量递增5%,同时,通过环保方式处理的垃圾量每年增加1.5万吨.为了确定处理生活垃圾的预算,请写出从今年起年内通过填埋方式处理的垃圾总量的计算公式,并计算从今年...