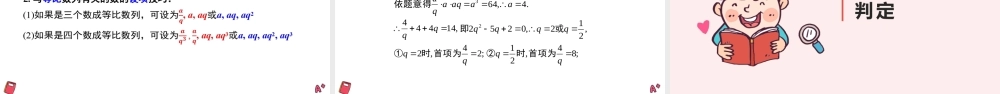4.3.1 等比数列的概念（教学课件）-2023-2024学年高二数学同步精品课堂（人教A版2019选择性必修第二册）.pptxVIP免费

选修第二册第四章《数列》4.3.1等比数列的概念我们知道，等差数列的特征是“从第2项起，每一项与它的前一项的差都等于同一个常数"，类比等差数列的研究思路和方法，从运算的角度出发，你觉得还有怎样的数列是值得研究的？实例3.在营养和生存空间没有限制的情况下，某种细菌每20min就通过分裂繁殖一代，那么一个这种细菌从第1次分裂开始，各次分裂产生的后代个数依次是：2，4，8，16，32，64，…⑤细菌个数第一次第二次第三次24第n次……分裂次数8实例4.某人存入银行a元，存期为5年，年利率为r，那么按照复利，他5年内每年末得到的本利和分别是：a(1＋r)，a(1＋r)²，a(1＋r)³，a(1＋r)4，a(1＋r)5⑥复利是指把前一期的利息和本金加在一起算作本金，再计算下一期的利息.类比等差数列的研究，你认为可以通过怎样的运算发现以下数列的取值规律？你发现了什么规律？.9,}{9102312aaaaaaan则表示数列①如果用取值规律：从第2项起，每一项与它的前一项的比都等于9．共同规律：从第2项起，每一项与前一项的比都等于同一个常数.新知1.等比数列的概念若一个数列从第2项起，每一项与它的前一项的比都等于同一个常数，则该数列叫等比数列；这个常数叫做公比，记为q(q≠0).为等比数列为非零常数②}{)(,1*nnnaqqaaNn)0(112312qqaaaaaaaannnn注：①等比数列的每一项和公比都不为0.如：1,1,1,1,…是等差数列，也是等比数列；0,0,0,0,…是等差数列，不是等比数列；),0()2,0(:11Nnqqaanqqaannnn或定义式非零常数列既是等差数列，又是等比数列，公差为0，公比为1.巩固：等比数列的概念1.判断下列数列是否是等差数列.如果是，写出它的公差.(1)3915212733;(2)11.11.211.33114641;111111(3);(4)48163264128.369121518，，，，，，，，，，，，，，，，，，，，不是；1.1是,公比为；不是；2.是,公比为(5)0,1,2,4,8,…(6)2,0,2,0,2,…不是；不是；(7)1,a,a2,a4,a8,…a≠0时，是等比数列，公比为aa=0时，不是等比数列;}{:1是常数列①naq)(}{:0正负项交替是摆动数列②naq所有的奇数项同号，所有的偶数项同号，但奇偶项异号等比数列的通项公式的推导daann1等差数列daadaadaadaadaadaa32143413231212类比qaann1等比数列31434213231212qaaqaaqaaqaaqaaqaa)0,(1qa不完全归纳法得an=a1+(n-1)d不完全归纳法得an=a1qn-1等比数列的通项...