3.2.2 奇偶性（教学课件）-【上好课】2022-2023学年高一数学同步备课系列（人教A版2019必修第一册）.pptxVIP免费

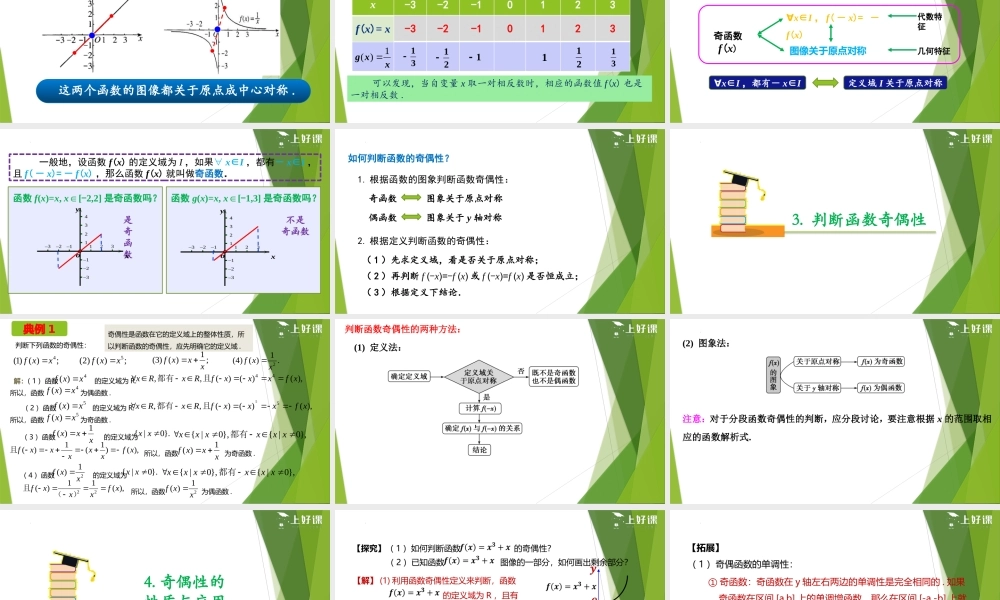
3.2.2奇偶性第3章函数的概念与性质人教A版2019必修第一册03判断函数奇偶性目录01.偶函数的概念和性质02.奇函数的概念和性质04奇偶性的性质与应用学习目标1、理解函数的奇偶性及其几何意义，培养数学抽象的核心素养；2、学会运用函数图象理解和研究函数的奇偶性，提升直观想象的核心素养；3、学会判断函数的奇偶性，强化逻辑推理的核心素养；4.在具体问题情境中，运用数形结合思想，利用奇偶性解决函数性质的总个问题，提升数学运算的核心素养。生活中的对称情景引入1.偶函数的概念和性质在平面直角坐标系中，利用描点法作出函数和的图象2xy2yx并观察这两个函数图象，总结出它们的共同特征。xyo12345-1123-1-2-3x…-3-2-10123…f(x)=x2……9410149x…-3-2-10123…f(x)=|x|……-101210-1xyo12345-1123-1-2-3图象关于y轴对称f(-1)f(1)f(-2)f(2)f(-3)f(3)===-xx(x.f(x))(-x,f(-x))f(-x)f(x)=任意一点x-3-2-10123f(x)=x2g(x)=2-|x|不妨取自变量的一些特殊值，观察相应函数值的情况，如下表：可以发现，当自变量x取一对相反数时，相应的函数值f(x)相等.9410149-101210-1观类比函数的单调性,你能用符号语言精确描述“函数图像关于y轴对称”的这种特征吗？（自变量与函数值之间的变化关系？）函数f(x)=x2,x[∈-2,2]是偶函数吗？函数g(x)=x2,x[∈-1,2]是偶函数吗？xy1234–1123–1–2–3oxy1234–1123–1o是偶函数不是偶函数一般地，设函数f(x)的定义域为I，如果∀x∈I，都有－x∈I，且f(－x)=f(x)，那么函数f(x)就叫做偶函数．偶函数f(x)一般地，设函数f(x)的定义域为I，如果∀x∈I，都有－x∈I，且f(－x)=f(x)，那么函数f(x)就叫做偶函数．∀x∈I，f(－x)=f(x)图像关于y轴对称代数特征几何特征∀x∈I，都有－x∈I定义域I关于原点对称-aaO),(aaO-aa),(),(aaOa-ab-b),(),(baab2.奇函数的概念和性质观察函数和的图象，并完成下面的两个函数值对应表，你能发现这两个函数有什么共同特征吗？xxf)(xxf1)(图象关于原点对称这两个函数的图像都关于原点成中心对称.x-3-2-10123f(x)=x为了用数学符号语言描述这一特征，不妨取自变量的一些特殊值，观察相应函数值的情况，如下表：可以发现，当自变量x取一对相反数时，相应的函数值f(x)也是一对相反数.-3-2-101232131213111xxg1)(一般地，设函数f(x)的定义域为I，如果∀x∈I，都有－x∈I，且f(－x)=－f(x)，那么函数f(x)就叫做奇函数．∀x∈I，f(－x)=－f(x)奇函数f(x)图像关于...