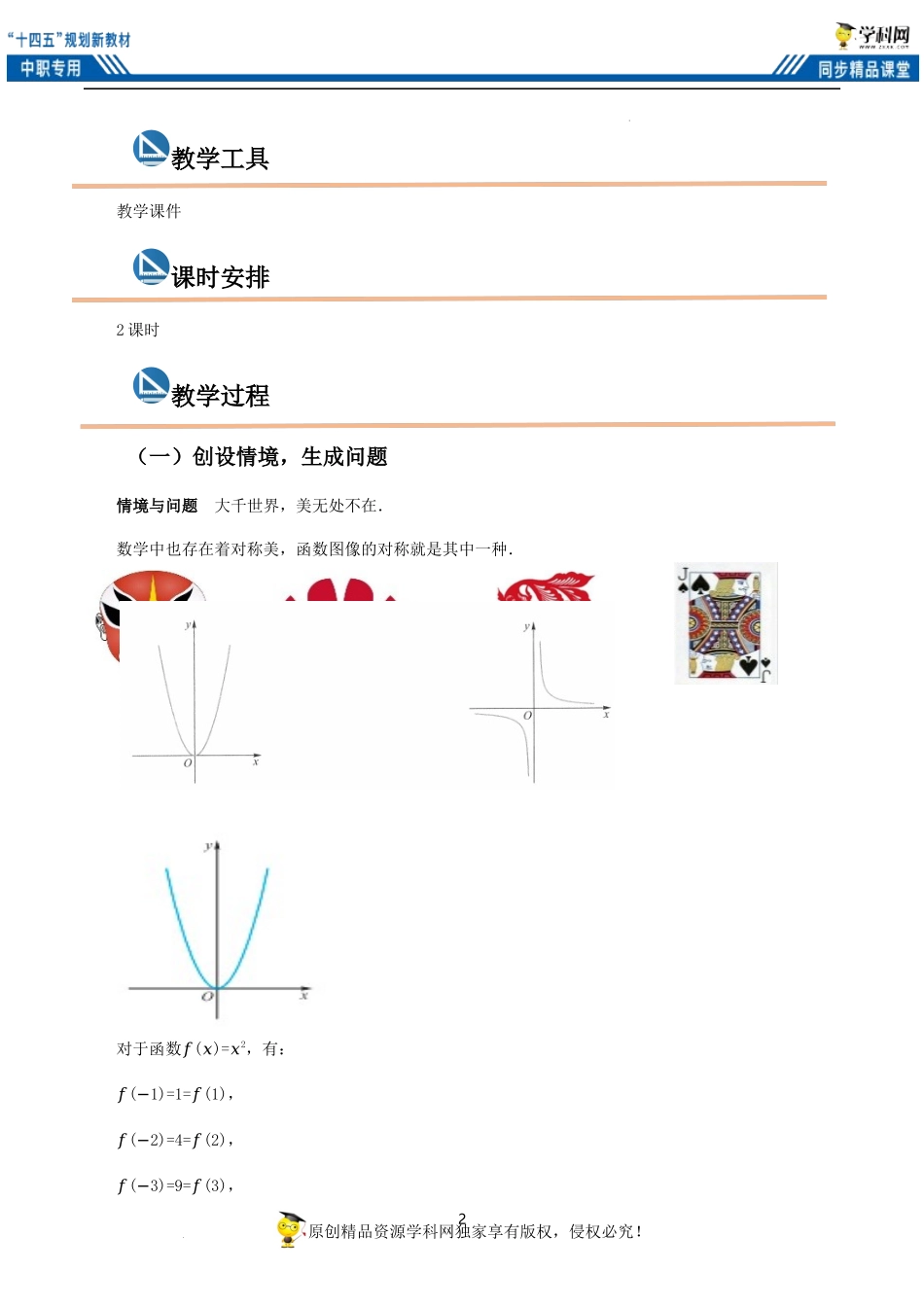
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司《3.3.2函数的奇偶性》教学设计学习目标学习重难点教材分析函数的奇偶性是函数的一条重要性质,教材从学生熟知的函数入手,结合初中学生已经学习过的轴对称和中心对称感受奇函数和偶函数的图像特征,从具体到抽象,注重信息技术的应用,比较系统地学习函数的奇偶性。奇偶性既是函数概念的拓展和深化,又是后续研究基本初等函数的基础在整个教材中起着承上启下的作用.学情分析从学生的认知基础看,学生在初中已经学习了轴对称图形和中心对称图形,并且有了一定数量的简单函数的储备。同时,刚刚学习了函数单调性,已经积累了研究函数的基本方法与初步经验.知识能力与素养⑴理解函数的奇偶性的概念;⑵理解具有奇偶性的函数的图像特征,会判断简单函数的奇偶性.⑴通过利用函数图像研究函数性质,培养学生的观察能力;⑵通过函数奇偶性的判断,培养学生的数据处理能力.重点难点⑴函数奇偶性的概念及其图像特征;⑵简单函数奇偶性的判定.函数奇偶性的判断.2原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司教学工具教学课件课时安排2课时教学过程(一)创设情境,生成问题情境与问题大千世界,美无处不在.数学中也存在着对称美,函数图像的对称就是其中一种.对于函数𝑓(𝑥)=𝑥2,有:𝑓(−1)=1=𝑓(1),𝑓(−2)=4=𝑓(2),𝑓(−3)=9=𝑓(3),3原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司……即对于定义域R上的任意一个𝑥,都有𝑓(−𝑥)=𝑥2=𝑓(𝑥).【设计意图】充分利用各种图形使学生领会图形的对称,生活中的对称图形也可以使学生感受数学的对称美(二)调动思维,探究新知设函数y=f(x)的定义域为数集D,若对于任意的x∈D,都有−x∈D,且f(−x)=f(x),则称y=f(x)是偶函数.偶函数的图像关于y轴对称.对于函数f(x)=1x有:f(−1)=−1=−f(1),f(−2)=−12=−f(2),f(−3)=−13=−f(3),……即对于定义域(−∞,0)∪(0,+∞)上的任意一个x,都有f(−x)=−1x=−f(x).4原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司设函数y=f(x)的定义域为数集D,若对于任意的x∈D,都有−x∈D,且f(−x)=−f(x),则称y=f(x)是奇函数.奇函数的图像关于原点中心对称.如果一个函数是奇函数或偶函数,就说这个函数具有奇偶性,其定义域一定关于原点中心对称.【设计意图】奇偶性的概念稍有抽象结合图像分析,仔细分...