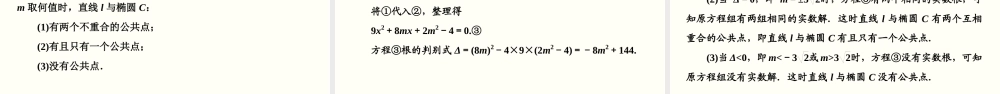3.1椭圆数学(人教版)选择性必修第一册第三章圆锥曲线的方程3.1.2椭圆的简单几何性质(第2课时素养目标学科素养1.进一步掌握椭圆的方程及其性质,会判断点与椭圆、直线与椭圆的位置关系;(重点)2.能运用直线与椭圆的位置关系解决相关的弦长、中点弦问题.(难点)1.数学运算;2.逻辑推理;3.数学建模情境导学1.设椭圆的两焦点为F1,F2,已知点P在椭圆上时,|PF1|+|PF2|=2a,那么点P在椭圆外时,设直线PF1交椭圆于Q,此时|PF1|+|PF2|与|QF1|+|QF2|的大小关系如何?2.直线与椭圆的位置关系,可否像讨论直线与圆的位置关系那样,将直线与椭圆的方程联立组成方程组,通过方程组的解的个数来讨论?第一阶段课前自学质疑情景导学感知新课1.点与椭圆的位置关系类比点与圆的位置关系,点P(x0,y0)与椭圆x2a2+y2b2=1(a>b>0)的位置关系的判定方法如下:点P在椭圆上⇔______________________;点P在椭圆内部⇔____________________;点P在椭圆外部⇔____________________.x20a2+y20b2=1x20a2+y20b2>1x20a2+y20b2<1必备知识深化预习2.直线y=kx+m与椭圆x2a2+y2b2=1(a>b>0)的位置关系直线y=kx+m与椭圆x2a2+y2b2=1(a>b>0)的位置关系判断方法,联立y=kx+m,x2a2+y2b2=1,消去y得到一个关于x的一元二次方程.位置关系解的个数Δ的取值相交________解Δ________0相切________解Δ________0相离________解Δ________0两>一=无<小题体验判断(正确的打“√”,错误的打“×”).(1)点A(1,1)在椭圆x24+y22=1的内部.()√解析:将A(1,1)代入椭圆方程,得x24+y22=34.因为34<1,所以点A在该椭圆内部.(2)已知椭圆x2a2+y2b2=1(a>b>0)与点P(b,0),过点P可作出该椭圆的一条切线.()×解析:因为点P(b,0)在椭圆的内部,所以过点P无法作出椭圆的切线.(3)直线x2-y=0被椭圆x24+y2=1截得的弦长为10.()√解析:直线与椭圆的两交点坐标分别为2,22和-2,-22,故弦长为10.1.已知点(2,3)在椭圆x2m2+y2n2=1上,则下列说法正确的是()A.点(-2,3)在椭圆外B.点(3,2)在椭圆上C.点(-2,-3)在椭圆内D.点(2,-3)在椭圆上D解析:由椭圆的对称性知,点(2,-3)在椭圆上,故选D.预习验收衔接课堂2.若直线l:2x+by+3=0过椭圆C:10x2+y2=10的一个焦点,则b的值是()A.-1B.12C.-1或1D.-12或12C解析:易知椭圆x2+y210=1的焦点为F1(0,-3),F2(0,3),所以b=1或-1.3.已知中心在坐...