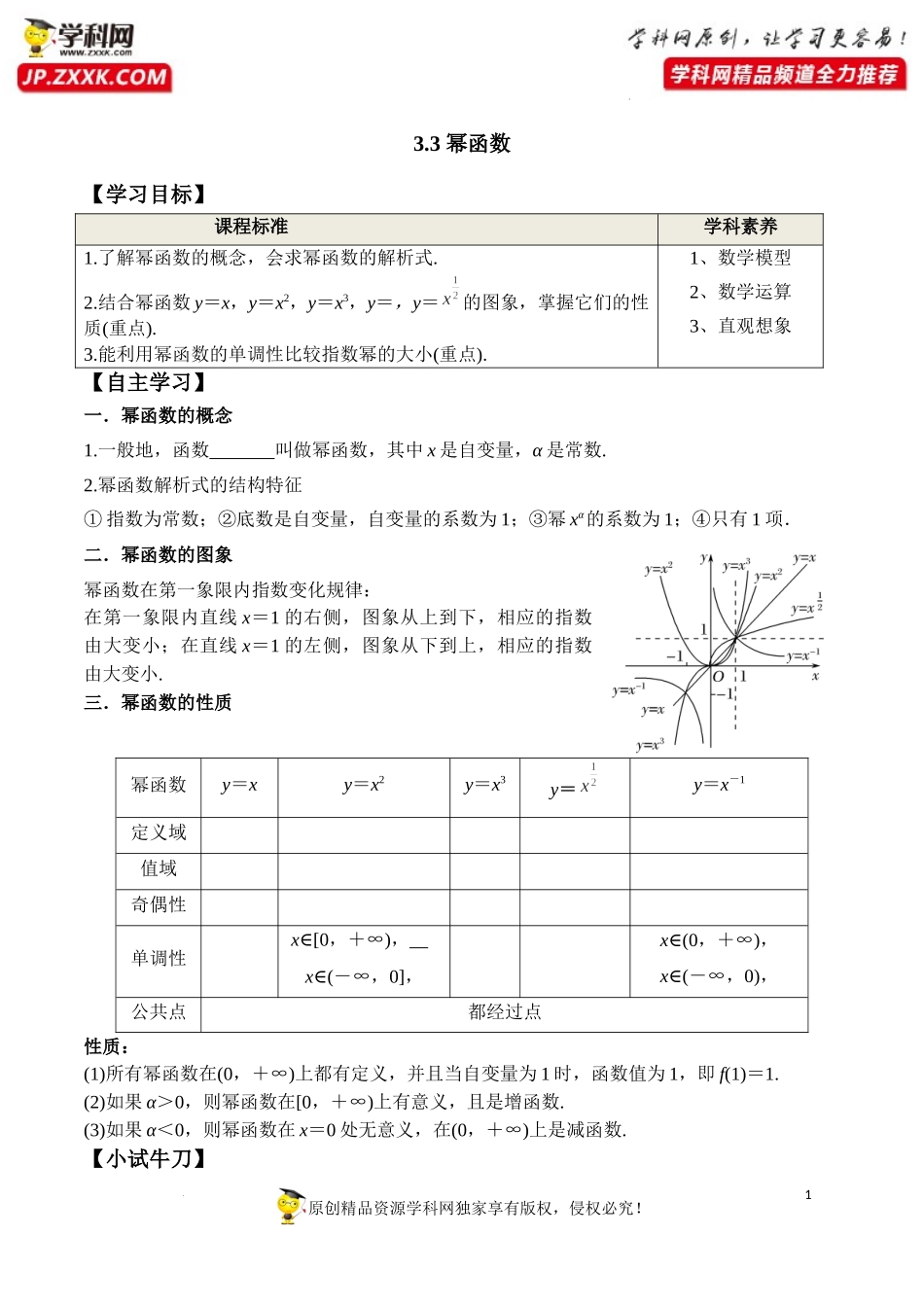
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司3.3幂函数【学习目标】课程标准学科素养1.了解幂函数的概念,会求幂函数的解析式.2.结合幂函数y=x,y=x2,y=x3,y=,y=的图象,掌握它们的性质(重点).3.能利用幂函数的单调性比较指数幂的大小(重点).1、数学模型2、数学运算3、直观想象【自主学习】一.幂函数的概念1.一般地,函数叫做幂函数,其中x是自变量,α是常数.2.幂函数解析式的结构特征①指数为常数;②底数是自变量,自变量的系数为1;③幂xα的系数为1;④只有1项.二.幂函数的图象幂函数在第一象限内指数变化规律:在第一象限内直线x=1的右侧,图象从上到下,相应的指数由大变小;在直线x=1的左侧,图象从下到上,相应的指数由大变小.三.幂函数的性质幂函数y=xy=x2y=x3y=y=x-1定义域值域奇偶性单调性x[0∈,+∞),x(∈-∞,0],x(0∈,+∞),x(∈-∞,0),公共点都经过点性质:(1)所有幂函数在(0,+∞)上都有定义,并且当自变量为1时,函数值为1,即f(1)=1.(2)如果α>0,则幂函数在[0,+∞)上有意义,且是增函数.(3)如果α<0,则幂函数在x=0处无意义,在(0,+∞)上是减函数.【小试牛刀】2原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司1.思辨解析(正确的打“√”,错误的打“×”)(1)函数y=x0(x≠0)是幂函数.()(2)幂函数的图象必过点(0,0)和(1,1).()(3)幂函数的图象都不过第二、四象限.()(4)当α>0时,y=xα是增函数.()2.下列函数为幂函数的是()A.y=2x3B.y=2x2-1C.y=D.y=【经典例题】题型一幂函数的概念点拨:判断一个函数是否为幂函数的依据是该函数是否为y=xα(α为常数)的形式,即函数的解析式为一个幂的形式,且需满足:(1)指数为常数;(2)底数为自变量;(3)系数为1.例1(1)在函数①y=,②y=x2,③y=2x,④y=1,⑤y=2x2,⑥y=中,是幂函数的是()A.①②④⑤B.③④⑥C.①②⑥D.①②④⑤⑥(2)函数是幂函数,且当x∈(0,+∞)时,f(x)是增函数,求f(x)的解析式.【跟踪训练】1若幂函数f(x)满足f(9)=3,则f(100)=________.题型二幂函数的图象及性质点拨:解决幂函数图象问题应把握的两个原则(1)依据图象高低判断幂指数大小,相关结论为:①在x∈(0,1)上,指数越大,幂函数图象越靠近x轴(简记为指大图低);②在x∈(1,+∞)上,指数越大,幂函数图象越远离x轴(简记为指大图高).(2)依据图象确定幂指数α与0,1的大小关系,即根据幂...