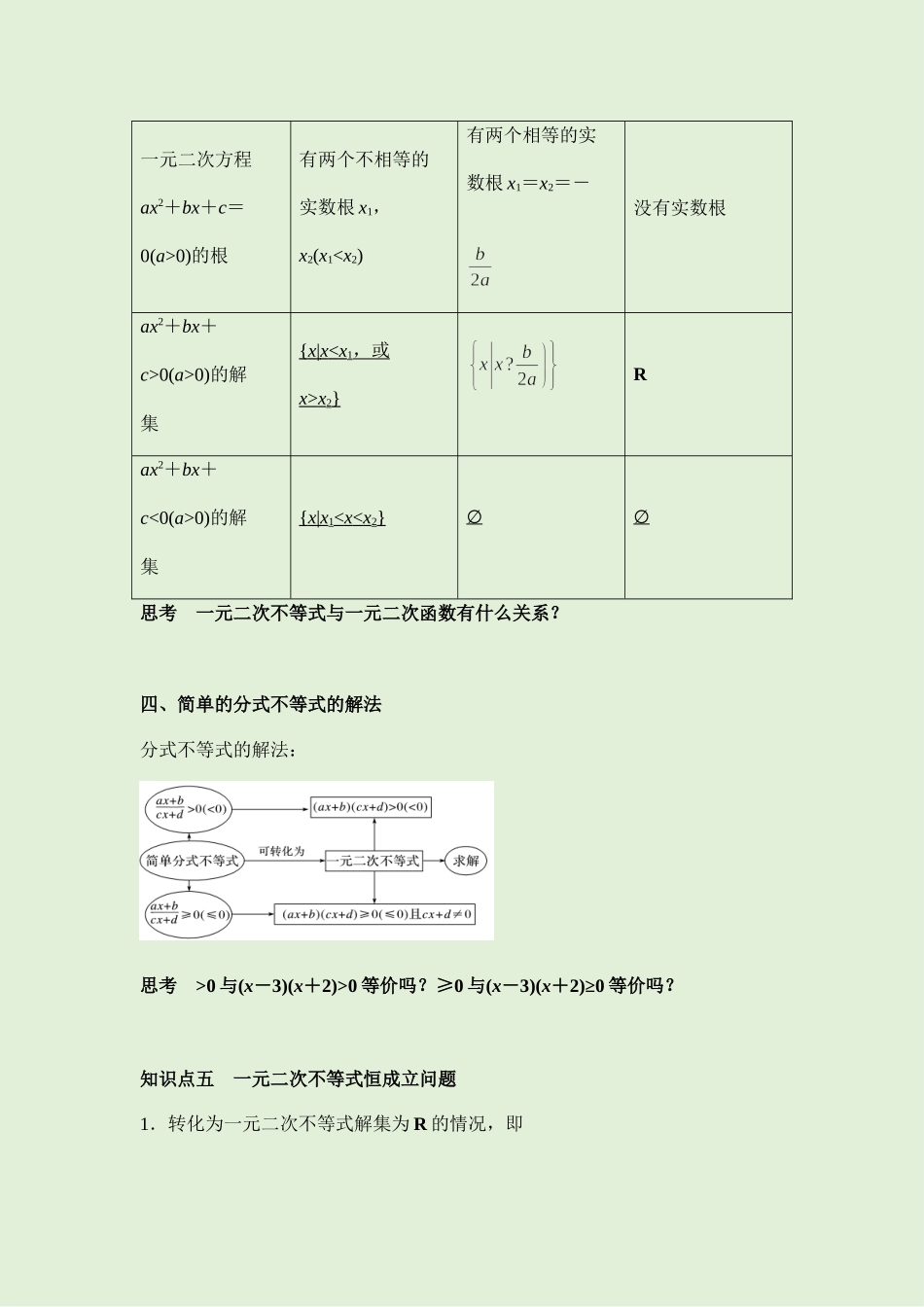
2.3二次函数和一元二次方程、不等式一、一元二次不等式的概念1.定义:只含有一个未知数,并且未知数的最高次数是2的不等式,叫做一元二次不等式2.一般形式:ax2+bx+c>0,ax2+bx+c<0,ax2+bx+c≥0,ax2+bx+c≤0,其中a≠0,a,b,c均为常数思考a2b+2ab2+9>0(ab≠0)可看作一元二次不等式吗?二、二次函数的零点一般地,对于二次函数y=ax2+bx+c,我们把使ax2+bx+c=0的实数x叫做二次函数y=ax2+bx+c的零点.思考二次函数y=x2-4的零点是什么?三、二次函数与一元二次方程、不等式的解的对应关系判别式Δ=b2-4acΔ>0Δ=0Δ<0二次函数y=ax2+bx+c(a>0)的图象一元二次方程ax2+bx+c=0(a>0)的根有两个不相等的实数根x1,x2(x10(a>0)的解集{x|xx2}Rax2+bx+c<0(a>0)的解集{x|x10与(x-3)(x+2)>0等价吗?≥0与(x-3)(x+2)≥0等价吗?知识点五一元二次不等式恒成立问题1.转化为一元二次不等式解集为R的情况,即ax2+bx+c>0(a≠0)恒成立⇔ax2+bx+c<0(a≠0)恒成立⇔2.分离参数,将恒成立问题转化为求最值问题.知识点六利用不等式解决实际问题的一般步骤1.选取合适的字母表示题目中的未知数.2.由题目中给出的不等关系,列出关于未知数的不等式(组).3.求解所列出的不等式(组).4.结合题目的实际意义确定答案.思考解一元二次不等式应用题的关键是什么?考点一解无参数一元二次不等式【例1】(2020·浙江高一课时练习)解不等式:.【练1】解下列不等式:(1);(2);(3);(4).(5)x2+3x-5>0(6)-2x2+3x-2<0;(7)-2<x2-3x≤10.考点二解含有参数的一元二次不等式【例2】(2020·怀仁市第一中学校云东校区高一期末(理))解关于的不等式:【练2】(2020·宁夏兴庆.银川一中高一期末)解关于的不等式:.考点三三个一元二次的关联【例3】(2020·农安县实验中学高一期末)已知关于的不等式的解集是,则的值是()A.B.11C.D.1【练3】(2020·全国高一开学考试)关于的不等式,解集为,则不等式的解集为()A.B.C.D.考点四一元二次的恒成立【例4】(2020·安徽省六安中学高二期末(文))若命题“存在,”为假命题,则实数的取值范围是____【练4】(2020·全国高一课时练习)当时,不等式恒成立,则实数的取值范围是_____________.考点五实际运用题【例5】...