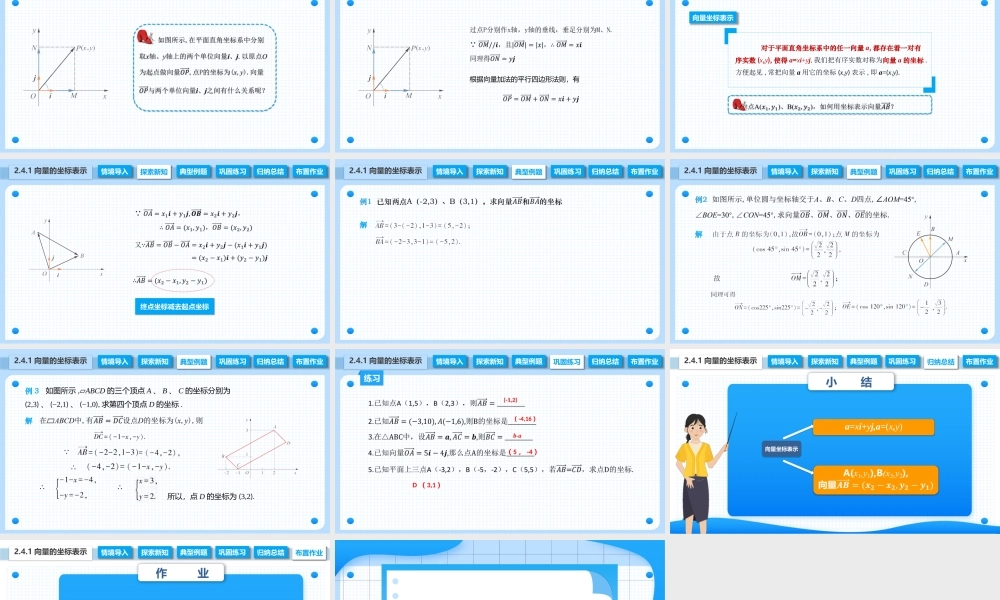
2.4.1向量的坐标表示中职数学拓展模块一上册探索新知典型例题巩固练习归纳总结布置作业2.4.1向量的坐标表示情境导入情境导入探索新知典型例题巩固练习归纳总结布置作业2.4.1向量的坐标表示情境导入情境导入根据向量加法的平行四边形法则,有情境导入典型例题巩固练习归纳总结布置作业2.4.1向量的坐标表示情境导入探索新知对于平面直角坐标系中的任一向量a,都存在着一对有序实数(x,y),使得a=xi+yj.我们把有序实数对称为向量a的坐标.方便起见,常把向量a用它的坐标(x,y)表示,即a=(x,y).向量坐标表示情境导入典型例题巩固练习归纳总结布置作业2.4.1向量的坐标表示情境导入探索新知终点坐标减去起点坐标情境导入典型例题情境导入探索新知巩固练习归纳总结布置作业2.4.1向量的坐标表示解情境导入典型例题情境导入探索新知巩固练习归纳总结布置作业2.4.1向量的坐标表示解情境导入典型例题情境导入探索新知巩固练习归纳总结布置作业解2.4.1向量的坐标表示例3如图所示,⏥ABCD的三个顶点A、B、C的坐标分别为(2,3)、(−2,1)、(−1,0),求第四个顶点D的坐标.∵∴所以,点D的坐标为(3,2).∴∴情境导入巩固练习情境导入探索新知典型例题归纳总结布置作业练习2.4.1向量的坐标表示(-1,2)(-4,16)b-a(5,-4)D(3,1)情境导入归纳总结情境导入探索新知典型例题巩固练习布置作业2.4.1向量的坐标表示小结向量坐标表示a=xi+yj,a=(x,y)情境导入布置作业情境导入探索新知典型例题巩固练习归纳总结2.4.1向量的坐标表示作业1.书面作业:完成教材第42、43页练习2.4.1;2.查漏补缺:根据个人情况对课堂学习复习与回顾;3.拓展作业:阅读教材扩展延伸内容.本节课堂结束.教师:姜老师