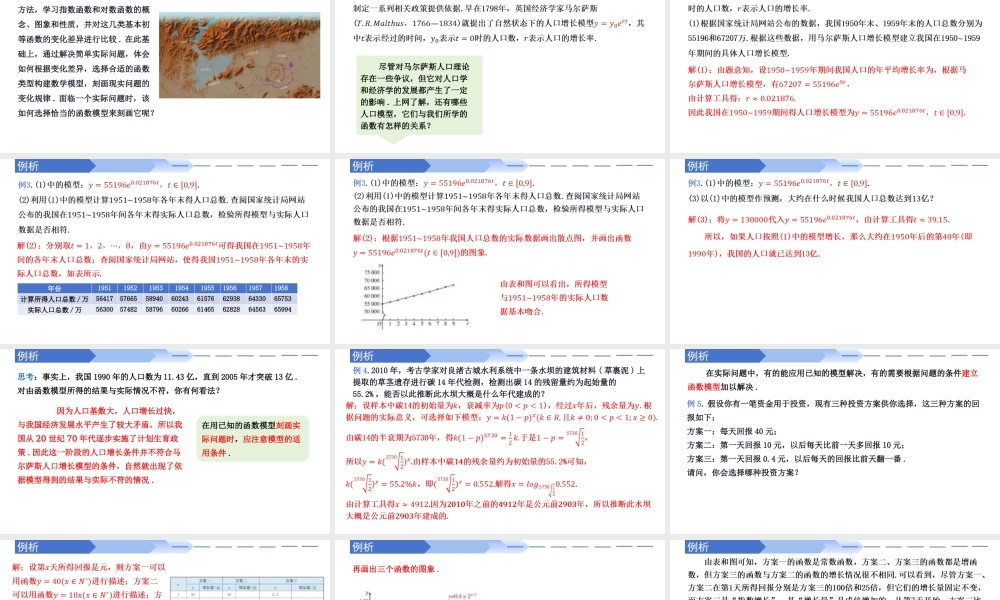
4.5函数的应用(二)4.5.3函数模型的应用第四章指数函数与对数函数复习引入在本章,我们类比幂函数的研究方法,学习指数函数和对数函数的概念、图象和性质,并对这几类基本初等函数的变化差异进行比较.在此基础上,通过解决简单实际问题,体会如何根据变化差异,选择合适的函数类型构建数学模型,刻画现实问题的变化规律.面临一个实际问题时,该如何选择恰当的函数模型来刻画它呢?例析尽管对马尔萨斯人口理论存在一些争议,但它对人口学和经济学的发展都产生了一定的影响.上网了解,还有哪些人口模型,它们与我们所学的函数有怎样的关系?例析例析年份19511952195319541955195619571958计算所得人口总数/万5641757665589406024361576629386433065753实际人口总数/万5630057482587966026661465628286456365994例析例析例析因为人口基数大,人口增长过快,与我国经济发展水平产生了较大矛盾,所以我国从20世纪70年代逐步实施了计划生育政策.因此这一阶段的人口增长条件并不符合马尔萨斯人口增长模型的条件,自然就出现了依据模型得到的结果与实际不符的情况.思考:事实上,我国1990年的人口数为11.43亿,直到2005年才突破13亿.对由函数模型所得的结果与实际情况不符,你有何看法?在用已知的函数模型刻画实际问题时,应注意模型的适用条件.例析例4.2010年,考古学家对良渚古城水利系统中一条水坝的建筑材料(草裹泥)上提取的草茎遗存进行碳14年代检测,检测出碳14的残留量约为起始量的55.2%,能否以此推断此水坝大概是什么年代建成的?例析在实际问题中,有的能应用已知的模型解决,有的需要根据问题的条件建立函数模型加以解决.例5.假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:方案一:每天回报40元;方案二:第一天回报10元,以后每天比前一天多回报10元;方案三:第一天回报0.4元,以后每天的回报比前天翻一番.请问,你会选择哪种投资方案?例析我们先用信息技术计算一下三种方案所得回报的增长情况(如下表).例析再画出三个函数的图象.函数图象是分析问题的好帮手.为了便于观察,用虚线连接离散的点.例析例析下面再看累计的回报数.通过信息技术列表如下.上述例子只是一种假想情况,但从中可以看到,不同的函数增长模型,增长变化存在很大差异.例析例析下面通过计算确认上述判断.先计算哪个模型的奖金总数不超过5万元.例析例析例析用函数建立数学模型解决实际问题的基本过程如下:这一过程包括分析和理解实际问题的...