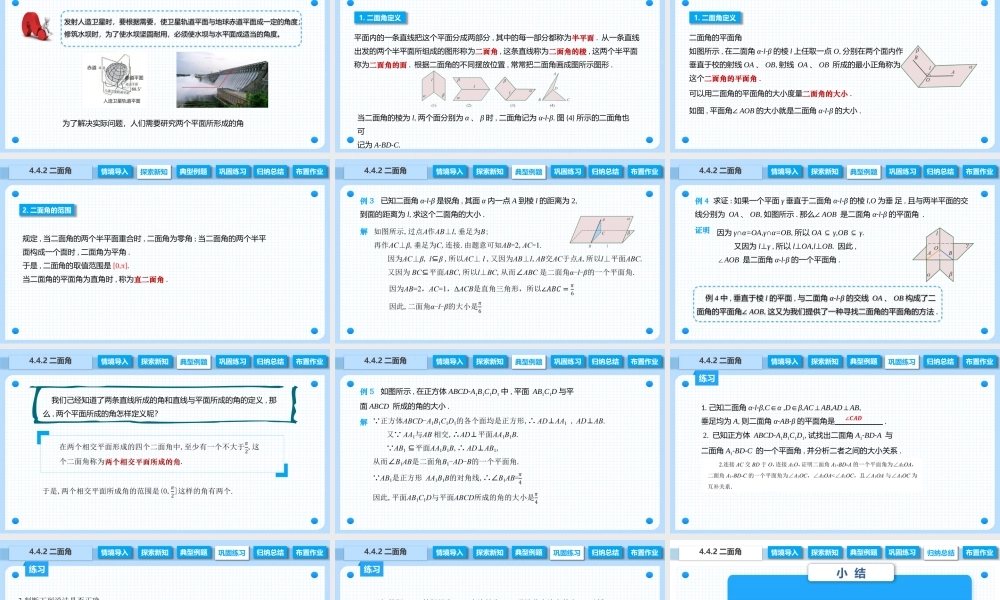
4.4.2二面角中职数学拓展模块一上册探索新知典型例题巩固练习归纳总结布置作业4.4.2二面角情境导入情境导入发射人造卫星时,要根据需要,使卫星轨道平面与地球赤道平面成一定的角度;修筑水坝时,为了使水坝坚固耐用,必须使水坝与水平面成适当的角度。为了解决实际问题,人们需要研究两个平面所形成的角情境导入典型例题巩固练习归纳总结布置作业4.4.2二面角情境导入探索新知1.二面角定义平面内的一条直线把这个平面分成两部分,其中的每一部分都称为半平面.从一条直线出发的两个半平面所组成的图形称为二面角,这条直线称为二面角的棱,这两个半平面称为二面角的面.根据二面角的不同摆放位置,常常把二面角画成图所示图形.当二面角的棱为l,两个面分别为α、β时,二面角记为α-l-β.图(4)所示的二面角也可记为A-BD-C.情境导入典型例题巩固练习归纳总结布置作业4.4.2二面角情境导入探索新知1.二面角定义二面角的平面角如图所示,在二面角α-l-β的棱l上任取一点O,分别在两个面内作垂直于校的射线OA、OB,射线OA、OB所成的最小正角称为这个二面角的平面角.如图,平面角∠AOB的大小就是二面角α-l-β的大小.可以用二面角的平面角的大小度量二面角的大小.情境导入典型例题巩固练习归纳总结布置作业4.4.2二面角情境导入探索新知2.二面角的范围规定,当二面角的两个半平面重合时,二面角为零角;当二面角的两个半平面构成一个面时,二面角为平角.于是,二面角的取值范围是[0,π].当二面角的平面角为直角时,称为直二面角.情境导入典型例题情境导入探索新知巩固练习归纳总结布置作业4.4.2二面角例3已知二面角α-l-β是锐角,其面α内一点A到棱l的距离为2,到面的距离为l,求这个二面角的大小.解情境导入典型例题情境导入探索新知巩固练习归纳总结布置作业4.4.2二面角例4求证:如果一个平面γ垂直于二面角α-l-β的棱l,O为垂足,且与两半平面的交线分别为OA、OB,如图所示.那么∠AOB是二面角α-l-β的平面角.证明因为γ∩α=OA,γ∩α=OB,所以OA⊆γ,OB⊆γ.又因为l⊥γ,所以l⊥OA,l⊥OB.因此,∠AOB是二面角α-l-β的一个平面角.例4中,垂直于棱l的平面,与二面角α-l-β的交线OA、OB构成了二面角的平面角∠AOB,这又为我们提供了一种寻找二面角的平面角的方法.情境导入典型例题情境导入探索新知巩固练习归纳总结布置作业4.4.2二面角我们己经知道了两条直线所成的角和直线与平面所成的角的定义,那么,两个平面所成的角怎样定义呢?情境导入典型例题情境导入探索新知巩固练习归纳总...