2.2.1 区间的概念课件-2022-2023学年高一上学期人教版(2021)中职数学基础模块上册.pptxVIP免费

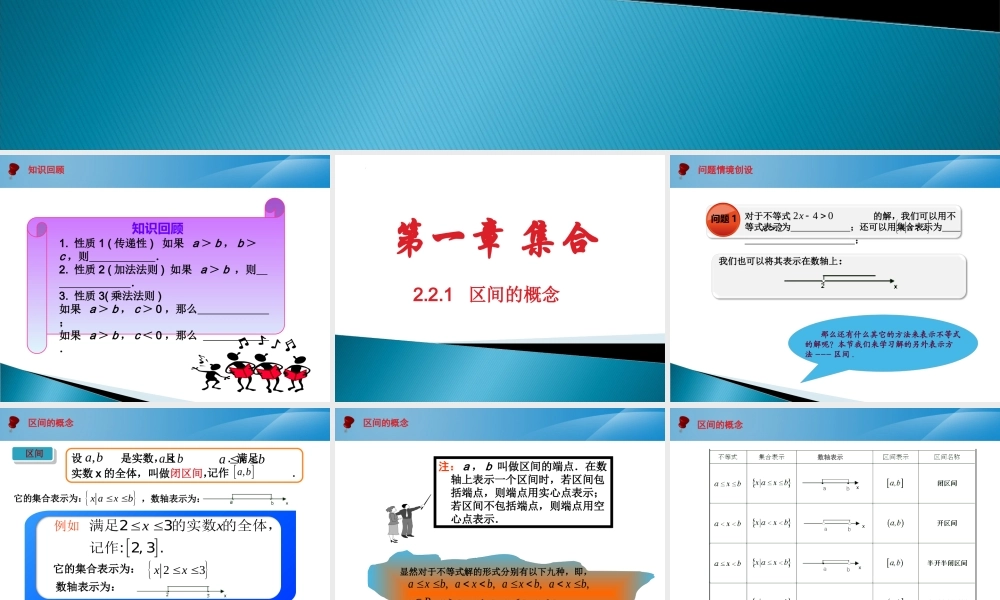
数学课程知识点10区间的概念知识回顾知识回顾1.性质1(传递性)如果a＞b，b＞c，则．2.性质2(加法法则)如果a＞b，则．3.性质3(乘法法则)如果a＞b，c＞0，那么；如果a＞b，c＜0，那么．第一章集合2.2.1区间的概念我们也可以将其表示在数轴上：那么还有什么其它的方法来表示不等式的解呢？本节我们来学习解的另外表示方法---区间.问题情境创设对于不等式的解，我们可以用不等式表示为；还可以用集合表示为；问题1240x2x2xx区间的概念区间设是实数，且.满足实数x的全体，叫做闭区间，,ababaxb记作.,abxaxb它的集合表示为：它的集合表示为：23xx数轴表示为：，数轴表示为：xx满足23的实数的全体，记作:2,3.例如区间的概念注：a，b叫做区间的端点．在数轴上表示一个区间时，若区间包括端点，则端点用实心点表示；若区间不包括端点，则端点用空心点表示．显然对于不等式解的形式分别有以下九种，即，我们通过如下表格来讲解.首先看前四种：,,,,,,,,.axbaxbaxbaxbxRxaxaxaxa区间的概念数轴表示区间的概念那么后四种不等式的形式可以用右侧表格来表示：全体实数也可以用区间表示为，符号“”读作“正无穷大”，“”读作“负无穷大”.,数轴表示例1用区间记法表示下列不等式的解集：(1)9≤x≤10；(2)x≤0.4．解：(1)[9，10]；(2)(－∞，0.4]．案例讲解课堂练习课堂练习用区间记法表示下列不等式的解集，并在数轴上表示这些区间：(1)－1≤x≤4；(2)－5＜x≤6；(3)－1≤x＜4；(4)－5＜x＜6；(5)x＞7；(6)x≤3．解：11,4,-14..x36,3,x.25,6,-56.。x31,4,-14。.x-56。。x45,6,57,,7。x例2用集合的性质描述法表示下列区间：(1)；(2)(－8，7]．4,0(2){x|1＜x≤4}．案例讲解练习用集合的性质描述法表示下列区间：(1)[－3，5)；(2)（1，4]．解：(1)；35xx(2){x|-8＜x≤7}．解：(1)；40xx例3在数轴上表示集合{x|x＜－2或x≥1}．解：如图所示．案例讲解课堂练习课堂练习已知数轴上的三个区间：(－∞，－3)，(－3，4)，(4，＋∞)．当x在每个区间上取值时，试确定代数式x＋3的值的符号．解：当时，即有，由不等式性质可得，所以x＋3在(－∞，－3)上的值的符号为负.,3x3x30x当时，即有，由不等式性质可得，所以x＋3在(－3，4)上的值的符号为正.3,4x3...