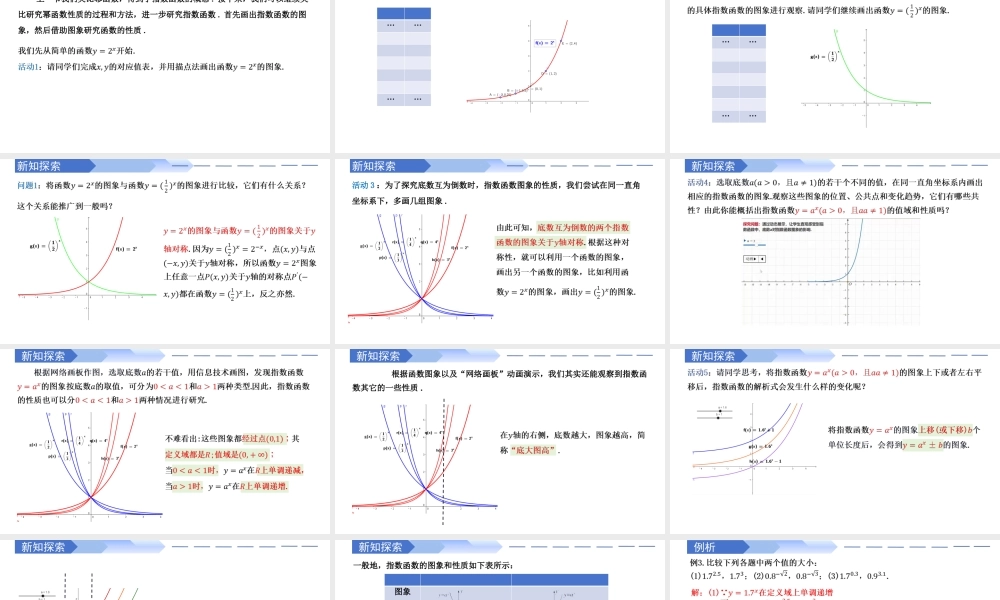
4.2.2指数函数的图象和性质第四章指数函数与对数函数活动引入上一节我们类比幂函数,得到了指数函数的概念.接下来,我们可以继续类比研究幂函数性质的过程和方法,进一步研究指数函数.首先画出指数函数的图象,然后借助图象研究函数的性质.新知探索…………新知探索…………新知探索新知探索活动3:为了探究底数互为倒数时,指数函数图象的性质,我们尝试在同一直角坐标系下,多画几组图象.新知探索新知探索新知探索根据函数图象以及“网络画板”动画演示,我们其实还能观察到指数函数其它的一些性质.新知探索新知探索新知探索一般地,指数函数的图象和性质如下表所示:图象定义域值域性质过定点,即时,减函数增函数当时,;当时,当时,;当时,与的图象关于轴对称例析由例3可以看到,利用指数函数的单调性,通过自变量的大小关系可以判断相应函数值的大小关系.例析例4.如图,某城市人口呈指数增长.(1)根据图象,估计该城市人口每翻一番所需的时间(倍增期);(2)该城市人口从80万人开始,经过20年会增长到多少万人?解:(1)观察图象,发现该城市人口经过20年约为10万人,经过40年约为20万人,即由10万人口增加到20万人口所用的时间约为20年,所以该城市人口每翻一番所需的时间约为20年.(2)因为倍增期为20年,所以每经过20年,人口将翻一番.因此,从80万人开始,经过20年,该城市人口大约会增长到160万人.练习题型一:指数函数的定义域和值域练习指数函数定义域、值域的处理技巧:(1)关注定义域,比如分母、奇(偶)次方根等;(2)关注值域,有时候需要分离系数、结合二次函数的性质求解,再结合着指数函数的单调性求解值域.练习练习题型二:指数函数的图象及应用练习指数函数图象问题的处理技巧:(1)抓住图象上的特殊点,如指数函数的图象恒过定点.(2)利用图象变换,如函数图象的平移变换(左加右减、上加下减).(3)利用函数的奇偶性与单调性.奇偶性决定函数图象的走势.练习练习题型三:利用指数函数性质比大小练习比较指数式大小的类型及处理方法:(1)底数相同,指数不同:利用指数函数的单调性来判断.(2)底数不同,指数相同:利用底数不同的指数函数的图象的变化规律来判断.(3)底数不同,指数不同:通过中间量来比较.练习练习题型四:利用指数函数性质解不等式练习练习课堂小结&作业课堂小结:(1)指数函数的图象性质;(2)求指数型函数的定义域和值域的一般方法;(3)比较指数式大小的类型及处理方法;(4)指数不等式的三种求解方法.作业:(1)整理本节...