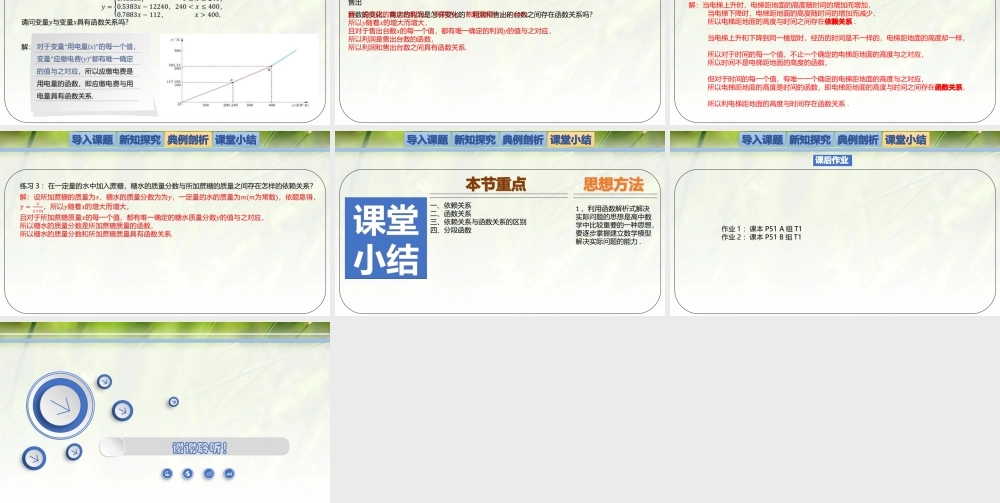
1生活中的变量关系北师大版(2019)高中数学必修第一册第二章函数第1节生活中的变量关系导入课题新知讲授典例剖析课堂小结像上面这样的变量关系,在实际生活中还有很多,摸清变量之间有何关系,能帮助我们解决很多生活中的问题,因此,今天我们要更加深入地学习生活中的变量关系.一、依赖关系导入课题依赖关系:在某变化过程中有两个变量,如果其中一个变量的值发生了变化,另一个变量的值也会随之发生变化,那么就称这两个变量具有依赖关系.新知探究典例剖析课堂小结一、依赖关系导入课题新知探究典例剖析课堂小结二、函数关系导入课题新知探究典例剖析课堂小结注意:凡是要确定两个变量具有函数关系,就要判断“对于变量x的每一个值,变量y都有唯一确定的值和它对应”.二、函数关系导入课题新知探究典例剖析课堂小结注意:凡是要确定两个变量具有函数关系,就要判断“对于变量x的每一个值,变量y都有唯一确定的值和它对应”.二、函数关系导入课题新知探究典例剖析课堂小结例4如表,记录了几个不同气压下水的沸点:沸点是气压的函数,即沸点与气压具有函数关系.“”“”对于变量气压的每一个值,变量沸点都有唯一确定的值和它对应.三、依赖关系与函数关系的区别导入课题新知探究典例剖析课堂小结1、函数关系一定是依赖关系,而依赖关系不一定是函数关系.2、要确定两变量是否有函数关系,需先分清谁是自变量,谁是因变量,当两个变量之间具有函数关系时,就不用再说它们之间还有依赖关系了.函数关系依赖关系四、分段函数导入课题分段函数:在自变量的不同取值范围内,因变量与自变量有不同的函数关系,需要用不同的解析式来表示的函数叫作分段函数.新知探究典例剖析课堂小结导入课题新知探究典例剖析课堂小结例5绿化可以改变小环境气候.某市有甲、乙两个气温观测点,观测点甲的绿化优于观测点乙,如图,是这两个观测点某一天的气温曲线图.为了方便比较,将两条曲线画在了同一平面直角坐标系中,如图所示,请问气温与时间具有函数关系吗?解:图中的两条曲线反映的都是“”对于时间“”的每一个值,都有唯一确定的气温值和它对应,所以每一条曲线都表示了一个函数关系,即气温是时间的函数,即气温与时间具有函数关系.导入课题新知探究典例剖析课堂小结解:导入课题新知探究典例剖析课堂小结练习1:某电器商店以2500元/台的价格购进了一批电视机,然后以2900元/台的价格售出,随着售出台数的变化,商店的利润是怎样变化的?利润和售出的台数之间存在...