2.2 基本不等式（含2课时）-2022-2023学年高一数学教材配套教学精品课件（人教A版2019必修第一册).pptxVIP免费

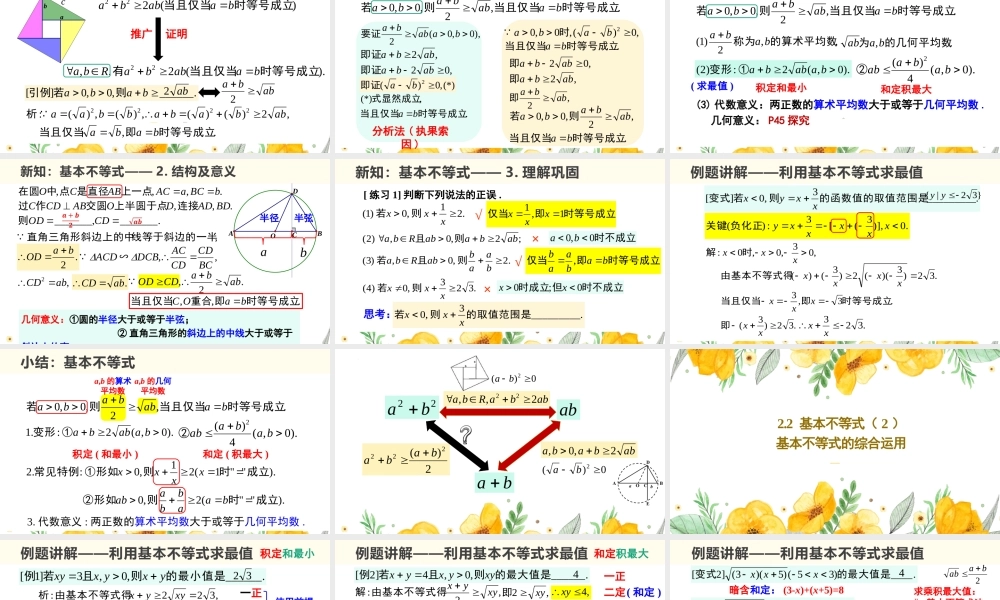
第二章《一元二次函数、方程和不等式》2.2基本不等式(1)新知引入：赵爽弦图与不等式abc)(222时等号成立当且仅当baabba推广证明).(2,,22时等号成立当且仅当有baabbaRba.______,0,0][baba则若引例,2)()(,)(,)(:2222abbababbaa析.,时等号成立即当且仅当babaab2abba2新知：基本不等式——1.证明(分析法).,2,0,0时等号成立当且仅当则若baabbaba),0,0(2baabba要证,2abba即证,02abba即证(*),0)(2ba即证.,(*)时等号成立当且仅当式显然成立ba分析法(执果索因),0)(,0,02baba时.时等号成立当且仅当ba,02abba即,2abba即,2abba即.,2,0,0时等号成立当且仅当则若baabbaba新知：基本不等式——2.结构及意义.,2,0,0时等号成立当且仅当则若baabbaba,,2)1(的算术平均数称为baba.,的几何平均数为baab(3)代数意义：两正数的算术平均数大于或等于几何平均数.几何意义：P45探究).0,(2:)2(baabba①变形).0,(4)(2babaab②积定和最小和定积最大(求最值)DBOAC.,,,bBCaACABCO上一点是直径点中在圆.,,BDADDOABCDC连接上半圆于点交圆作过.______________,CDOD则ab,2abCD.abCD.2,abbaCDOD.,,时等号成立即重合当且仅当baOC半径半弦新知：基本不等式——2.结构及意义几何意义：①圆的半径大于或等于半弦；②直角三角形的斜边上的中线大于或等于斜边上的高,,BCCDCDACDCBACD∽,线等于斜边的一半直角三角形斜边上的中.2baOD新知：基本不等式——3.理解巩固[练习1]判断下列说法的正误..323,0)4(xxx则若√×时等号成立即仅当1,1xxx×时不成立0,0ba.21,0)1(xxx则若;2,0,)2(abbaabRba则且时不成立但时成立0;0xx.2,0,)3(baababRba则且若时等号成立即仅当babaab,√._________3,0的取值范围是则若xxx思考：例题讲解——利用基本不等式求最值._________3,0][的函数值的取值范围是则若变式xxyx,03,0,0:xxx时解.3,3时等号成立即当且仅当xxx.32)3(xx即.323xx.0)],3([3:)(xxxxxy负化正关键.32)3)((2)3()(xxxx由基本不等式得}32|{yy小结：基本不等式3.代数意义:两正数的算术平均数大于或等于几何平均数.).0,(2:.1baabba①变形).0,(4)(2babaab②.,2,0,...