3.3.2 抛物线的简单几何性质（教学课件）-2023-2024学年高二数学同步精品课堂（人教A版2019选择性必修第一册）.pptxVIP免费

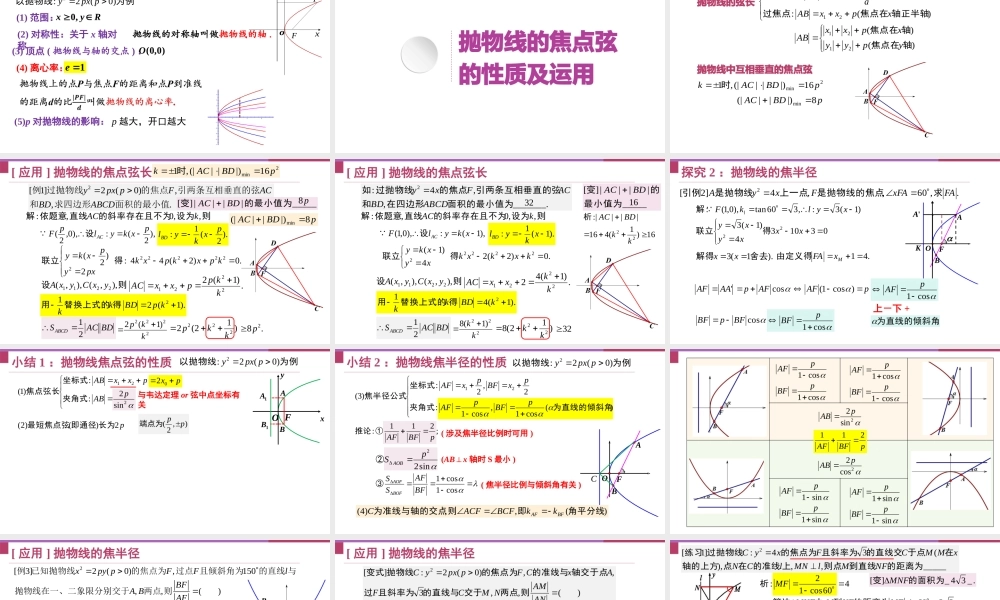
3.3.2抛物线的简单几何性质为例以抛物线)0(2:2ppxy(1)范围：Ryx,0(2)对称性：关于x轴对称抛物线的对称轴叫做抛物线的轴.(3)顶点(抛物线与轴的交点)：)0,0(O(4)离心率：1eyoxFP(5)p对抛物线的影响：p越大，开口越大1.抛物线的简单几何性质抛物线的焦点弦的性质及运用抛物线的弦长)(:1:212轴正半轴焦点在过焦点不过焦点xpxxABakAB)()(2121轴焦点在轴焦点在ypyyxpxxAB抛物线中互相垂直的焦点弦2min16|)||(|,1pBDACk时pBDAC8|)||(|min[应用]抛物线的焦点弦长则设为的斜率存在且不为直线依题意解,,0,:kAC),2(:),0,2(pxkylpFAC设.0)2(44:2)2(222222kpxkpxkpxypxky得联立则设),,(),,(2211yxCyxA.)1(22221kkppxxAC).1(212kpBDkk得替换上式的用BDACSABCD212222)1(2kkp)12(2222kkp.82p2[1]2(0),,.ypxpFACBDABCD例过抛物线的焦点引两条互相垂直的弦和求四边形面积的最小值).2(1:pxkylBD2min16|)||(|,1pBDACk时_____||||][的最小值为变BDACp8pBDAC8|)||(|min[应用]抛物线的焦点弦长则设为的斜率存在且不为直线依题意解,,0,:kAC),1(:),0,1(xkylFAC设则设),,(),,(2211yxCyxA.)1(422221kkxxAC).1(412kBDkk得替换上式的用BDACSABCD21222)1(8kk)12(822kk32._______,,4:2面积的最小值为在四边形和引两条互相垂直的弦的焦点过抛物线如ABCDBDACFxy).1(1:xkylBD_____||||][最小值为的变BDAC3216)1(416|||:|22kkBDAC析16.0)2(24)1(22222kxkxkxyxky得联立探究2：抛物线的焦半径.,60,,4]2[2FAxFAFxyA求是抛物线的焦点上一点是抛物线引例031034)1(3)1(3:,360tan),0,1(:22xxxyxyxylkFl得联立解).1(3舍去解得xx.41MxFA由定义得BOFA'AK'AAAFcosAFppAF)cos1(cos1pAFcosBFpBFcos1pBF.为直线的倾斜角上－下+小结1：抛物线焦点弦的性质为例以抛物线)0(2:2ppxy与韦达定理or弦中点坐标有关p2)()2(长为即通径最短焦点弦xOyFAB1A1B),2(pp端点为221sin2::)1(pABpxxAB夹角式坐标式焦点弦长px02小结2：抛物线焦半径的性质为例以抛物线)0(2:2ppxyBOFA)(cos1,cos1:2,2:...