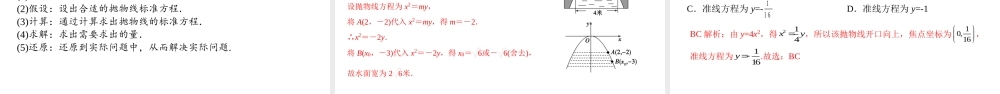第三章圆锥曲线的方程3.3.1抛物线及其标准方程学习目标素养目标学科素养1.掌握抛物线的定义及焦点、准线的概念.(重点)2.掌握抛物线的标准方程及其推导过程.(易错点)3.明确p的几何意义,并能解决简单的求抛物线标准方程问题.(难点)1、直观想象2、数学运算3、逻辑推理一.抛物线的定义平面内与一个定点F和一条定直线l(l不经过点F)的距离的点的轨迹叫做抛物线.点F叫做抛物线的,直线l叫做抛物线的.相等焦点准线自主学习思考1:抛物线的定义中,若点F在直线l上,那么点的轨迹是什么?点的轨迹是过点F且垂直于直线l的直线.自主学习二.抛物线的标准方程图形标准方程焦点坐标准线方程y2=2px(p>0)Fp2,0x=-p2y2=-2px(p>0)x2=2py(p>0)F0,p2y=-p2x2=-2py(p>0)F-p2,0x=p2F0,-p2y=p2自主学习思考2:抛物线方程中p(p>0)的几何意义是什么?p的几何意义是焦点到准线的距离.自主学习1.思考辨析(正确的打“√”,错误的打“×”)(1)抛物线的方程都是二次函数.()(2)抛物线的焦点到准线的距离是p.()(3)平面内到一定点距离与到一定直线距离相等的点的轨迹一定是抛物线.()(4)y=4x2的焦点坐标为(1,0).()(5)以(0,1)为焦点的抛物线的标准方程为x2=4y.()2.已知动点P到定点(0,2)的距离和它到直线l:y=-2的距离相等,则点P的轨迹方程为________.√×√××x2=8y小试牛刀题型一求抛物线的标准方程例1根据下列条件分别求出抛物线的标准方程:(1)准线方程为y=23;(2)焦点在y轴上,焦点到准线的距离为5.解:(1)易知抛物线的准线交y轴于正半轴,且p2=23,则p=43,故所求抛物线的标准方程为x2=-83y.(2)已知抛物线的焦点在y轴上,可设方程为x2=2my(m≠0),由焦点到准线的距离为5,知|m|=5,m=±5,所以满足条件的抛物线有两条,它们的标准方程分别为x2=10y和x2=-10y.经典例题总结求抛物线标准方程的方法1.定义法:根据定义求p,最后写标准方程;2.待定系数法:设标准方程,列有关的方程组求系数;3.直接法:建立恰当的坐标系,利用抛物线的定义列出动点满足的条件,列出对应方程,化简方程.题型一求抛物线的标准方程经典例题跟踪训练1根据下列条件分别求出抛物线的标准方程:(1)经过点(-3,-1);(2)焦点为直线3x-4y-12=0与坐标轴的交点.解:(1)因为点(-3,-1)在第三象限,所以设所求抛物线的标准方程为y2=-2px(p>0)或x2=-2py(p>0).若抛物线的标准方程为y2=-2px(p>0),...