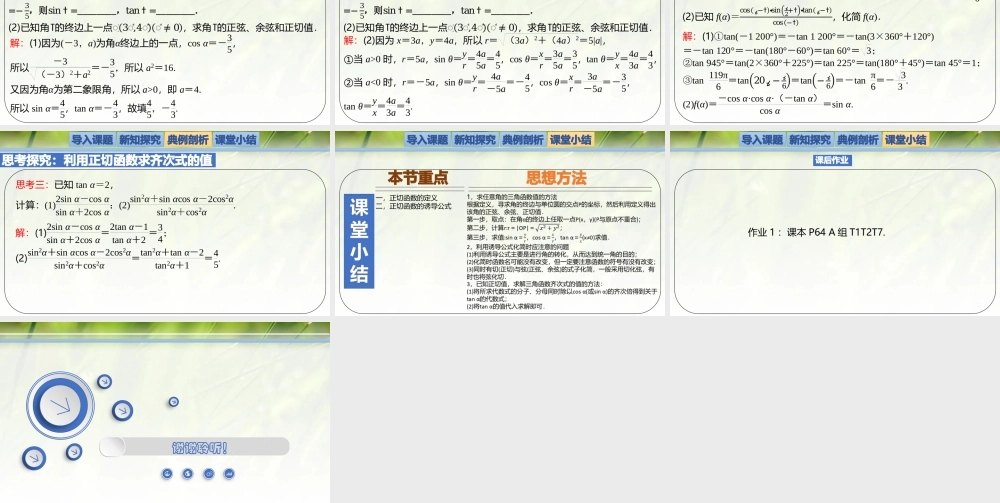
7.1-7.2正切函数的定义及其诱导公式北师大版(2019)高中数学必修第二册第一章三角函数第7节正切函数导入课题新知讲授典例剖析课堂小结在初中,我们就学习过正弦函数、余弦函数、正切函数,并把正切函数定义为直角三角形中对边与邻边的比.在前两节中,我们重新定义了正弦函数和余弦函数,并借助它们的图象研究其性质,同时也对正弦函数和余弦函数的诱导公式进行了深入探究.那么正切函数又该如何定义的呢?正切函数的诱导公式又是什么样的呢?探究一导入课题新知探究典例剖析课堂小结一、正切函数的定义导入课题新知探究典例剖析课堂小结探究二导入课题思考:前面我们学习了正、余弦函数的诱导公式,那么正切函数有诱导公式吗?试着写一写.新知探究典例剖析课堂小结导入课题新知探究典例剖析课堂小结二、正切函数的诱导公式导入课题新知探究典例剖析课堂小结二、正切函数的诱导公式导入课题新知探究典例剖析课堂小结教材P58例题例2如图设角α的终边上任取一点Q(x,y)(x≠0),求角α的正切函数值.导入课题新知探究典例剖析课堂小结教材P58例题导入课题新知探究典例剖析课堂小结教材P60例题导入课题新知探究典例剖析课堂小结思考探究:正切函数的定义思考一:(1)已知角ߙ的终边上一点坐标为(-3,a),且ߙ为第二象限角,cosߙ=−35,则sinߙ=________,tanߙ=________.(2)已知角ߠ的终边上一点ܲ�3ܲ�,4ܲ�ܲ�≠0,求角ߠ的正弦、余弦和正切值.解:(1)因为(-3,a)为角α终边上的一点,cosα=-35,所以-3(-3)2+a2=-35,所以a2=16.又因为角α为第二象限角,所以a>0,即a=4.所以sinα=45,tanα=-43,故填45,-43.导入课题新知探究典例剖析课堂小结思考探究:正切函数的定义思考一:(1)已知角ߙ的终边上一点坐标为(-3,a),且ߙ为第二象限角,cosߙ=−35,则sinߙ=________,tanߙ=________.(2)已知角ߠ的终边上一点ܲ�3ܲ�,4ܲ�ܲ�≠0,求角ߠ的正弦、余弦和正切值.解:(2)因为x=3a,y=4a,所以r=(3a)2+(4a)2=5|a|,①当a>0时,r=5a,sinθ=yr=4a5a=45,cosθ=xr=3a5a=35,tanθ=yx=4a3a=43,②当a<0时,r=-5a,sinθ=yr=4a-5a=-45,cosθ=xr=3a-5a=-35,tanθ=yx=4a3a=43.导入课题新知探究典例剖析课堂小结思考探究:正切函数的诱导公式思考二:(1)求下列三角函数值:①tan(-1200°);②tan945°;③tan119π6.(2)已知f(α)=cosߨ−ߙ∙sinߨ2+ߙ∙tanߨ−ߙcos−ߙ,化简f(α).解:(1...