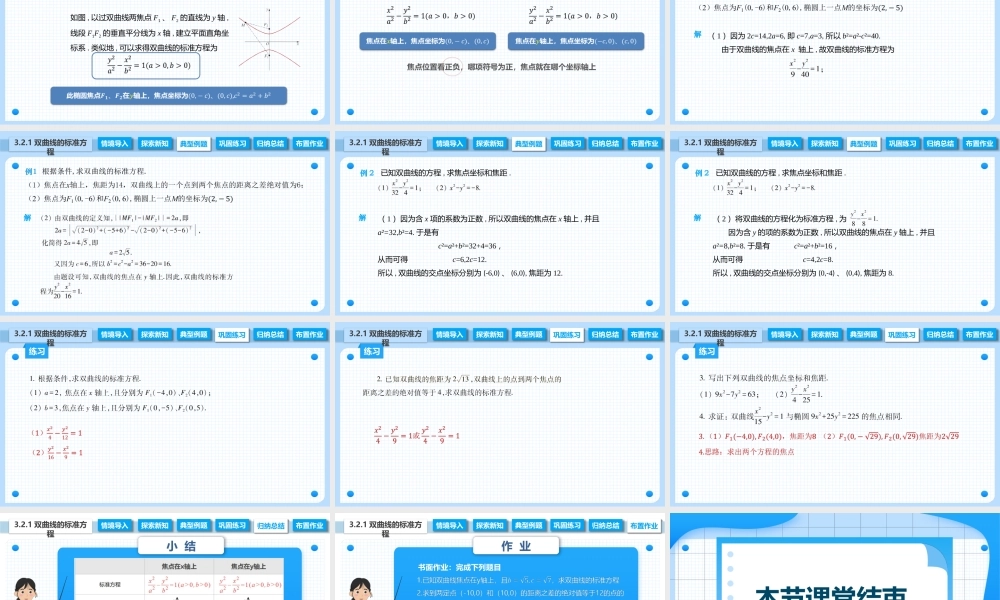
3.2.1双曲线的标准方程中职数学拓展模块一上册探索新知典型例题巩固练习归纳总结布置作业3.2.1双曲线的标准方程情境导入情境导入广州塔是目前世界上已经建成的最高的塔桅建筑,广州塔的两侧轮廓线是什么图形?有什么特点?可以看出,广州塔两侧的轮廓线是关于塔中轴对称的两条曲线,它们分别从塔的腰部向上下两个方向延伸,人们称这样的曲线为双曲线.那么,如何画出双曲线呢?情境导入典型例题巩固练习归纳总结布置作业3.2.1双曲线的标准方程情境导入探索新知实验探究双曲线(1)取一条拉链,把它拉开分成两条,将其中一条剪短.把长的一条的端点固定在点F1处,短的一条的端点固定在点F2处;(2)将笔尖放在拉链锁扣M处,随着拉链的拉开或闭合,笔尖就画出一条曲线(图中右边的曲线);(3)再把拉链短的一条的端点固定在点F1处,长的一条的端点固定在点F2处.类似地,笔尖可面出另一条曲线(图中左边的曲线).情境导入典型例题巩固练习归纳总结布置作业3.2.1双曲线的标准方程情境导入探索新知拉链是不可伸缩的,笔尖(即点M)在移动过程中,与两个点F1、F2的距离之差的绝对值始终保特不变.一般地,把平面内与两个定点F1、F2的距离之差的绝对值为常数(小于|F1F2|)的点的轨迹称为双曲线.这两个定点称为双曲线的焦点,两焦点之间的距离称为双曲线的焦距.1.双曲线的定义情境导入典型例题巩固练习归纳总结布置作业3.2.1双曲线的标准方程情境导入探索新知一般地,把平面内与两个定点F1、F2的距离之差的绝对值为常数(小于|F1F2|)的点的轨迹称为双曲线.这两个定点称为双曲线的焦点,两焦点之间的距离称为双曲线的焦距.1.双曲线的定义注意:0椭圆定义符号表示情境导入典型例题巩固练习归纳总结布置作业3.2.1双曲线的标准方程情境导入探索新知2.双曲线的标准方程建系以经过双曲线两焦点F1、F2的直线为x轴,以线段F1F2的垂直平分线为y轴,建立平面直角坐标系,如图所示.情境导入典型例题巩固练习归纳总结布置作业3.2.1双曲线的标准方程情境导入探索新知2.双曲线的标准方程设点设M(x,y)为双曲线上的任一点,双曲线的焦距为2c(c>0),则焦点F1、F2的坐标分别为(-c,0)、(c,0).情境导入典型例题巩固练习归纳总结布置作业3.2.1双曲线的标准方程情境导入探索新知2.双曲线的标准方程限制条件代坐标情境导入典型例题巩固练习归纳总结布置作业3.2.1双曲线的标准方程情境导入探索新知2.双曲线的标准方程化简移项平方,去根号移项并整理情境导入典型例题巩固练习归纳总结布置作业3.2.1双曲线的标准方程情...