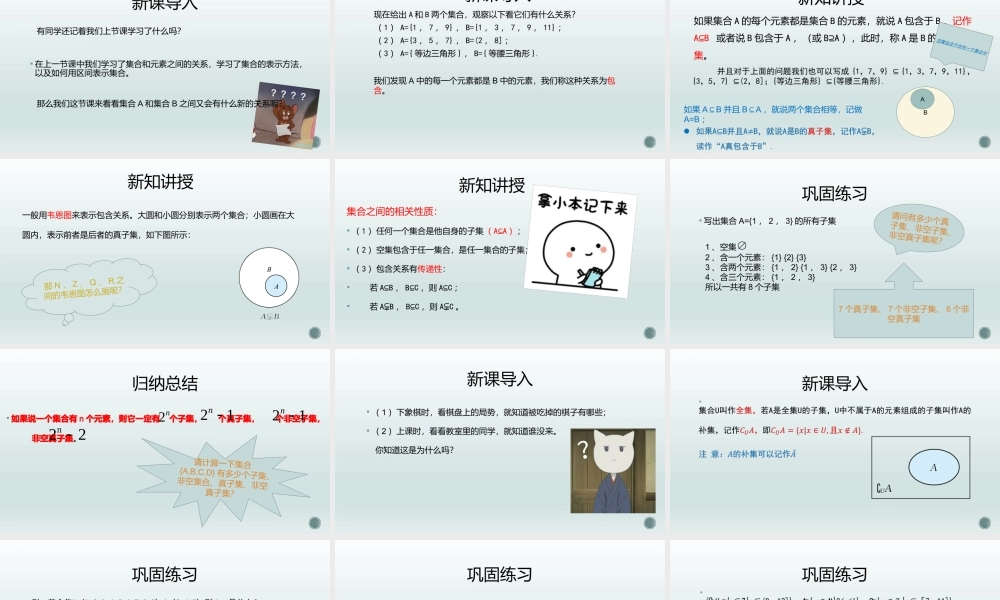
1.1集合1.1.2子集和补集新课导入在上一节课中我们学习了集合和元素之间的关系,学习了集合的表示方法,以及如何用区间表示集合。有同学还记着我们上节课学习了什么吗?那么我们这节课来看看集合A和集合B之间又会有什么新的关系呢?新课导入现在给出A和B两个集合,观察以下看它们有什么关系?(1)A={1,7,9},B={1,3,7,9,11};(2)A={3,5,7},B=(2,8];(3)A={等边三角形},B={等腰三角形}.我们发现A中的每一个元素都是B中的元素,我们称这种关系为包含。新知讲授如果集合A的每个元素都是集合B的元素,就说A包含于B,记作AB⊆或者说B包含于A,(或BA⊇),此时,称A是B的一个子集。BA如果AB⊆并且BA⊆,就说两个集合相等,记做A=B;新知讲授一般用韦恩图来表示包含关系。大圆和小圆分别表示两个集合;小圆画在大圆内,表示前者是后者的真子集,如下图所示:那N,Z,Q,R之间的韦恩图怎么画呢?新知讲授集合之间的相关性质:(1)任何一个集合是他自身的子集(AA⊆);(2)空集包含于任一集合,是任一集合的子集;(3)包含关系有传递性:若AB⊆,BC⊆,则AC⊆;若A⫋B,BC⊆,则A⫋C。巩固练习写出集合A={1,2,3}的所有子集1、空集∅2、含一个元素:{1}{2}{3}3、含两个元素:{1,2}{1,3}{2,3}4、含三个元素:{1,2,3}所以一共有8个子集请问有多少个真子集、非空子集、非空真子集呢?7个真子集、7个非空子集、6个非空真子集归纳总结如果说一个集合有n个元素,则它一定有个子集,个真子集,个非空子集,非空真子集。2n21nn2221n请计算一下集合{A,B,C,D}有多少个子集、非空集合、真子集、非空真子集?新课导入(1)下象棋时,看棋盘上的局势,就知道被吃掉的棋子有哪些;(2)上课时,看看教室里的同学,就知道谁没来。你知道这是为什么吗?新课导入巩固练习巩固练习巩固练习归纳总结课后练习拔高训练作业布置例4设{Z(0,12)}Uxx,{20212,N}Axxx,{33[1,11],BxxZ}x,求UAð和UBð.谢谢大家数学课到此结束