2.5.1直线与圆的位置关系课件-2022-2023学年高二上学期数学人教A版（2019）选择性必修第一册.pptxVIP免费

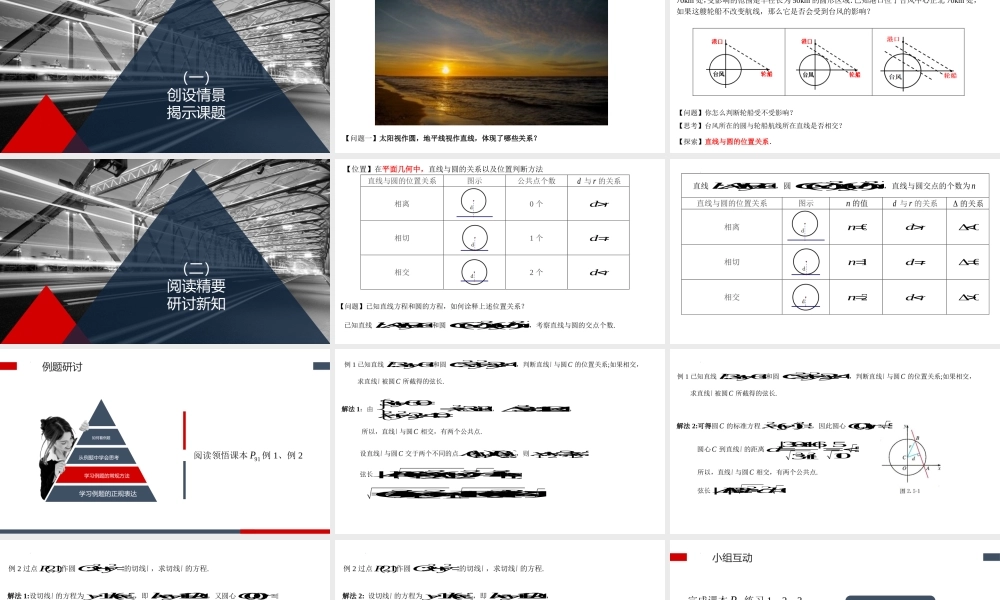
第二章2.5.1直线与圆的位置关系直线和圆的方程凯里一中尹洪January26,2025（一）创设情景揭示课题【情景一】太阳在一天内与地平线的关系【问题一】太阳视作圆，地平线视作直线，体现了哪些关系？【问题】你怎么判断轮船受不受影响？【情景二】台风与轮船的航行一艘轮船在沿直线返回港口的途中，接到气象台的台风预报：台风中心位于轮船正西70km处，受影响的范围是半径长为50km的圆形区域．已知港口位于台风中心正北70km处，如果这艘轮船不改变航线，那么它是否会受到台风的影响？【思考】台风所在的圆与轮船航线所在直线是否相交？【探索】直线与圆的位置关系．（二）阅读精要研讨新知【问题】已知直线方程和圆的方程，如何诠释上述位置关系？【位置】在平面几何中，直线与圆的关系以及位置判断方法直线与圆的位置关系图示公共点个数d与r的关系相离0个rd相切1个rd相交2个rd已知直线:0lAxByC和圆222:()()Cxaybr，考察直线与圆的交点个数.直线:0lAxByC，圆222:()()Cxaybr，直线与圆交点的个数为n直线与圆的位置关系图示n的值d与r的关系的关系相离0nrd0相切1nrd0相交2nrd0例题研讨学习例题的正规表达学习例题的常规方法从例题中学会思考如何看例题阅读领悟课本91P例1、例2解法1：由222360320240xyxxxyy，2341210，所以，直线l与圆C相交，有两个公共点.例1已知直线:360lxy和圆22:240Cxyy，判断直线l与圆C的位置关系;如果相交，求直线l被圆C所截得的弦长.设直线l与圆C交于两个不同的点1122(,),(,)AxyBxy，则12123,2xxxx弦长222121212||()()1||ABxxyykxx22221212(1)[()4][1(3)](342)10kxxxx解法2:可得圆C的标准方程22(1)5xy，因此圆心(0,1),5Cr圆心C到直线l的距离22|3016|551031d例1已知直线:360lxy和圆22:240Cxyy，判断直线l与圆C的位置关系;如果相交，求直线l被圆C所截得的弦长.所以，直线l与圆C相交，有两个公共点.弦长22||210ABrd解法1:设切线l的方程为1(2)ykx，即120kxyk，又圆心(0,0),1Or由2|12|11kdrk，解得0,k或43k因此，所求切线l的方程为1y,或4350xy.例2过点(2,1)P作圆22:1Oxy的切线l，求切线l的方程.解法2:设切线l的方程为1(2)ykx，即120kxyk，由2222221(2)(1)(24)4401y...