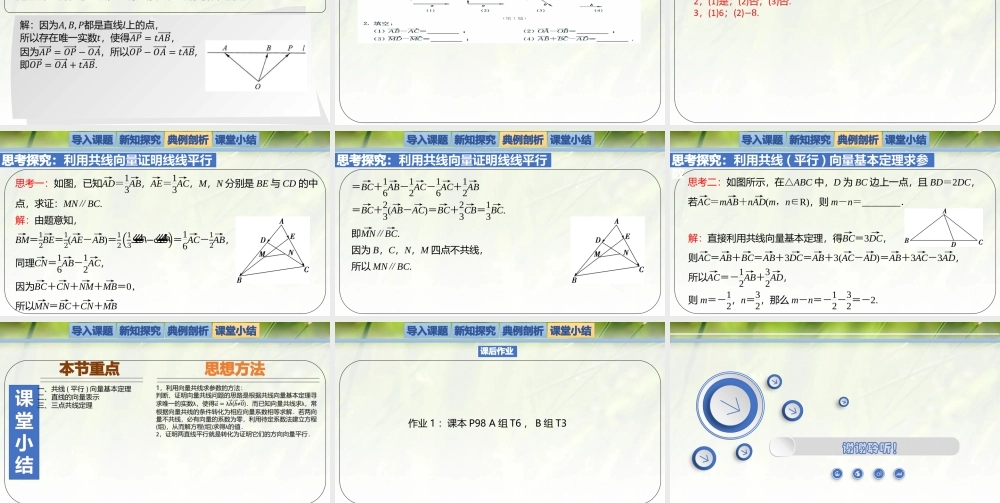
3.2向量的数乘与向量共线的关系北师大版(2019)高中数学必修第二册第二章平面向量及其应用第3节从速度的倍数到向量的数乘导入课题新知讲授典例剖析课堂小结在疾风暴雨、雷电交加的夜晚,为什么我们总是先看到闪电,后听到雷声?这是因为光速远远大于声速,经测量光速大小约为声速的8.8×10倍.速度的大小有倍数关系,同样向量的模也有倍数关系,今天我们就一起来学习向量模长的倍数关系.探究一导入课题新知探究典例剖析课堂小结一、共线(平行)向量基本定理导入课题新知探究典例剖析课堂小结探究二导入课题思考:通过前面的学习,我们知道,我们用有向线段来表示向量,那么反之,能否用向量来刻画直线呢?新知探究典例剖析课堂小结二、直线的向量表示导入课题新知探究典例剖析课堂小结探究三导入课题新知探究典例剖析课堂小结二、三点共线定理导入课题新知探究典例剖析课堂小结导入课题新知探究典例剖析课堂小结教材P95例题导入课题新知探究典例剖析课堂小结教材P95例题导入课题新知探究典例剖析课堂小结教材P96例题导入课题新知探究典例剖析课堂小结教材P97练习导入课题新知探究典例剖析课堂小结教材P97练习导入课题新知探究典例剖析课堂小结思考探究:利用共线向量证明线线平行思考一:如图,已知AD→=13AB→,AE→=13AC→,M,N分别是BE与CD的中点,求证:MN∥BC.解:由题意知,BM→=12BE→=12(AE→-AB→)=1213ܥܣԦሬሬሬ−ܤܣԦሬሬሬሬ=16AC→-12AB→,同理CN→=16AB→-12AC→,因为BC→+CN→+NM→+MB→=0,所以MN→=BC→+CN→+MB→导入课题新知探究典例剖析课堂小结思考探究:利用共线向量证明线线平行=BC→+16AB→-12AC→-16AC→+12AB→=BC→+23(AB→-AC→)=BC→+23CB→=13BC→.即MN→∥BC→.因为B,C,N,M四点不共线,所以MN∥BC.导入课题新知探究典例剖析课堂小结思考探究:利用共线(平行)向量基本定理求参数思考二:如图所示,在△ABC中,D为BC边上一点,且BD=2DC,若AC→=mAB→+nAD→(m,n∈R),则m-n=________.解:直接利用共线向量基本定理,得BC→=3DC→,则AC→=AB→+BC→=AB→+3DC→=AB→+3(AC→-AD→)=AB→+3AC→-3AD→,所以AC→=-12AB→+32AD→,则m=-12,n=32,那么m-n=-12-32=-2.导入课题新知探究典例剖析课堂小结课堂小结本节重点思想方法一、共线(平行)向量基本定理二、直线的向量表示三、三点共线定理导入课题新知探究典例剖析课堂小结课后作业作业1:课本P98A组T6,B组T3谢谢聆听!