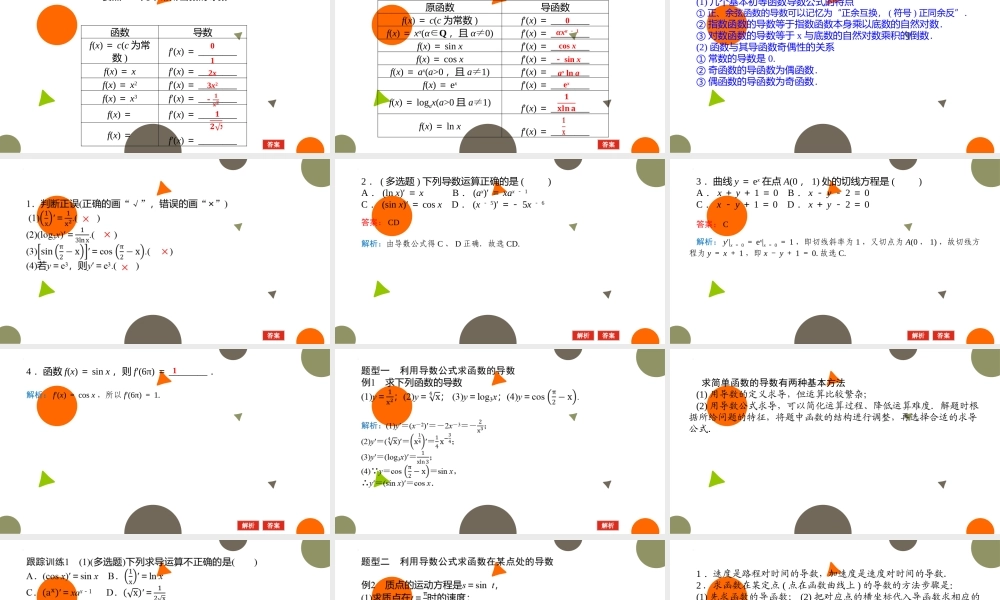
§3导数的计算南阳市五中要点一几个常用函数的导数函数导数f(x)=c(c为常数)f′(x)=________f(x)=xf′(x)=________f(x)=x2f′(x)=________f(x)=x3f′(x)=________f(x)=f′(x)=________f(x)=f′(x)=________012x3x2要点二基本初等函数的导数公式原函数导函数f(x)=c(c为常数)f′(x)=________f(x)=xα(α∈Q,且α≠0)f′(x)=________f(x)=sinxf′(x)=________f(x)=cosxf′(x)=________f(x)=ax(a>0,且a≠1)f′(x)=________f(x)=exf′(x)=________f(x)=logax(a>0且a≠1)f′(x)=________f(x)=lnxf′(x)=________0αxα-1cosx-sinxaxlnaex(1)几个基本初等函数导数公式的特点①正、余弦函数的导数可以记忆为“正余互换,(符号)正同余反”.②指数函数的导数等于指数函数本身乘以底数的自然对数.③对数函数的导数等于x与底数的自然对数乘积的倒数.(2)函数与其导函数奇偶性的关系①常数的导数是0.②奇函数的导函数为偶函数.③偶函数的导函数为奇函数.××××2.(多选题)下列导数运算正确的是()A.(lnx)′=xB.(ax)′=xax-1C.(sinx)′=cosxD.(x-5)′=-5x-6答案:CD解析:由导数公式得C、D正确.故选CD.3.曲线y=ex在点A(0,1)处的切线方程是()A.x+y+1=0B.x-y-2=0C.x-y+1=0D.x+y-2=0答案:C解析:y′|x=0=ex|x=0=1,即切线斜率为1,又切点为A(0,1),故切线方程为y=x+1,即x-y+1=0.故选C.4.函数f(x)=sinx,则f′(6π)=________.1解析:f′(x)=cosx,所以f′(6π)=1.求简单函数的导数有两种基本方法(1)用导数的定义求导,但运算比较繁杂;(2)用导数公式求导,可以简化运算过程、降低运算难度.解题时根据所给问题的特征,将题中函数的结构进行调整,再选择合适的求导公式.1.速度是路程对时间的导数,加速度是速度对时间的导数.2.求函数在某定点(点在函数曲线上)的导数的方法步骤是:(1)先求函数的导函数;(2)把对应点的横坐标代入导函数求相应的导数值.答案:(1)D(2)见解析求曲线方程或切线方程时的三点注意1.切点是曲线与切线的公共点,切点坐标既满足曲线方程也满足切线方程;2.曲线在切点处的导数就是切线的斜率;3.必须明确已知点是不是切点,如果不是,应先设出切点.跟踪训练3已知直线y=kx是y=lnx的一条切线,求k的值.易错辨析求切线方程时忽略“过”与“在”的差异致误例4经过点P(2,8)作曲线y=x3的切线,求切线方程.答案:ACD答案:A答案:C4.曲线y=lnx与x轴交点处的切线方程是________.y=x-15.当常数k为何值时,直线y=x与曲线y=x2+k相切?请求出切点.