3.3.1 抛物线及其标准方程（教学课件）-2023-2024学年高二数学同步精品课堂（人教A版2019选择性必修第一册）.pptxVIP免费

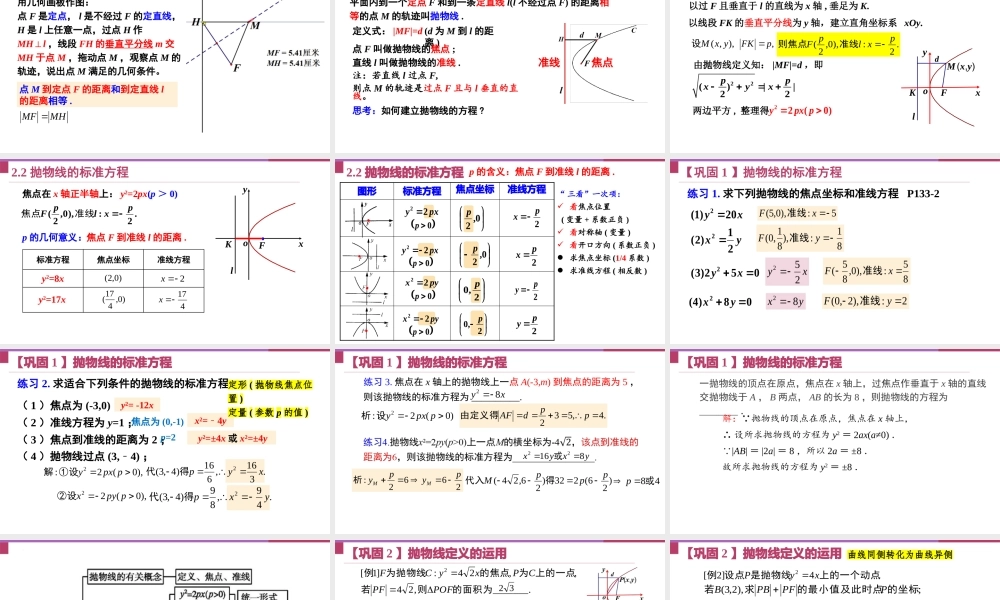
3.3.1抛物线及其标准方程用几何画板作图：点F是定点，l是不经过F的定直线，H是l上任意一点，过点H作MH⊥l，线段FH的垂直平分线m交MH于点M，拖动点M，观察点M的轨迹，说出点M满足的几何条件。数学小实验点M到定点F的距离和到定直线l的距离相等.lMHMF1.抛物线的定义平面内到一个定点F和到一条定直线l(l不经过点F)的距离相等的点M的轨迹叫抛物线.定义式：|MF|=d(d为M到l的距离)注：若直线l过点F,则点M的轨迹是过点F且与l垂直的直线。点F叫做抛物线的焦点;直线l叫做抛物线的准线.焦点准线思考：如何建立抛物线的方程?以过F且垂直于l的直线为x轴,垂足为K.22()||22ppxyx两边平方,整理得22(0)ypxp以线段FK的垂直平分线为y轴，建立直角坐标系xOy.由抛物线定义知：|MF|=d，即),,(yxM设,pFK.2:),0,2(pxlpF准线则焦点2.1推导抛物线的标准方程lxKyoMF(x,y)d焦点在x轴正半轴上：y2=2px(p＞0)p的几何意义：xyolFK2.2抛物线的标准方程焦点F到准线l的距离..2:),0,2(pxlpF准线焦点)0,2(2x标准方程焦点坐标准线方程y2=8x)0,417(417xy2=17x图形标准方程焦点坐标准线方程pxy220ppxy220ppyx220ppyx220p0,2p2px0,2p2px2,0p2py2,0p2py“三看”一次项：看焦点位置(变量+系数正负)看对称轴(变量)看开口方向(系数正负)求焦点坐标(1/4系数)求准线方程(相反数)2.2抛物线的标准方程p的含义：焦点F到准线l的距离.【巩固1】抛物线的标准方程xy20)1(2yx21)2(2052)3(2xy08)4(2yx5:),0,5(xF准线81:),81,0(yF准线xy25285:),0,85(xF准线2:),2,0(yF准线yx82练习1.求下列抛物线的焦点坐标和准线方程P133-2练习2.求适合下列条件的抛物线的标准方程.（1）焦点为(-3,0)；（2）准线方程为y=1；（3）焦点到准线的距离为2；y²=-12xx²=4﹣y（4）抛物线过点(3,4)﹣；y²=±4x或x²=±4y焦点为(0,-1)p=2【巩固1】抛物线的标准方程),0(2:2ppxy①设解),0(22ppyx②设.316,616)4,3(2xyp得代.49,89)4,3(2yxp得代定形(抛物线焦点位置)定量(参数p的值)练习3.焦点在x轴上的抛物线上一点A(-3,m)到焦点的距离为5，则该抛物线的标准方程为__________.)0(2:2ppxy设析.4,532ppdAF由定义得xy822662:pypyMM析)26(232)26,24(pppM得代入48或pyxyx...