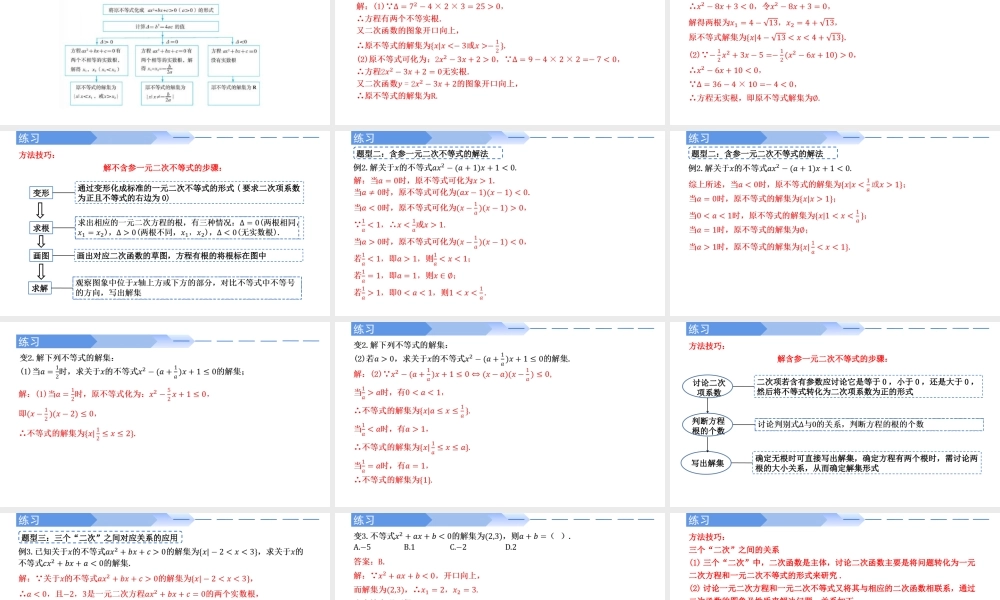
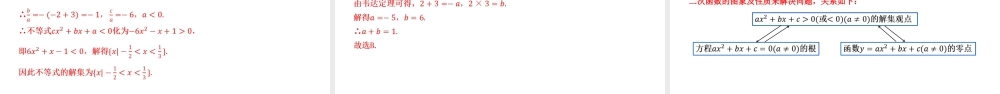2.3二次函数与一元二次方程、不等式第1课时问题导入在初中,我们从一次函数的角度看一元一次方程、一元一次不等式,发现了三者之间的内在联系,利用这种关系可以更好地解决相关问题.对于二次函数、一元二次方程和一元二次不等式,是否也有这样的联系呢?先来看一个问题.新知探索思考1:在初中,我们从一次函数的观点看一元一次方程、一元一次不等式的思想方法.类似地,能否从二次函数的观点看一元二次不等式,进而得到一元二次不等式的求解方法呢?新知探索新知探索新知探索二次函数与一元二次方程、不等式的解的对应关系的图象的根有两个不相等的实数根()有两个不相等的实数根没有实数根的解集或的解集例析例析例析新知探索现在,你能解决第2.1节的“问题2”了吗?利用框图可以清晰地表示求解一元二次不等式的过程.这里,我们以求解可化成形式的不等式为例,用框图表示其求解过程.练习题型一:不含参一元二次不等式的解法练习练习方法技巧:解不含参一元二次不等式的步骤:变形通过变形化成标准的一元二次不等式的形式(要求二次项系数为正且不等式的右边为0)求根画图画出对应二次函数的草图,方程有根的将根标在图中求解练习题型二:含参一元二次不等式的解法练习题型二:含参一元二次不等式的解法练习练习练习方法技巧:解含参一元二次不等式的步骤:讨论二次项系数二次项若含有参数应讨论它是等于0,小于0,还是大于0,然后将不等式转化为二次项系数为正的形式判断方程根的个数写出解集确定无根时可直接写出解集,确定方程有两个根时,需讨论两根的大小关系,从而确定解集形式练习题型三:三个“二次”之间对应关系的应用练习练习方法技巧:三个“二次”之间的关系(1)三个“二次”中,二次函数是主体,讨论二次函数主要是将问题转化为一元二次方程和一元二次不等式的形式来研究.(2)讨论一元二次方程和一元二次不等式又将其与相应的二次函数相联系,通过二次函数的图象及性质来解决问题,关系如下:课堂小结&作业