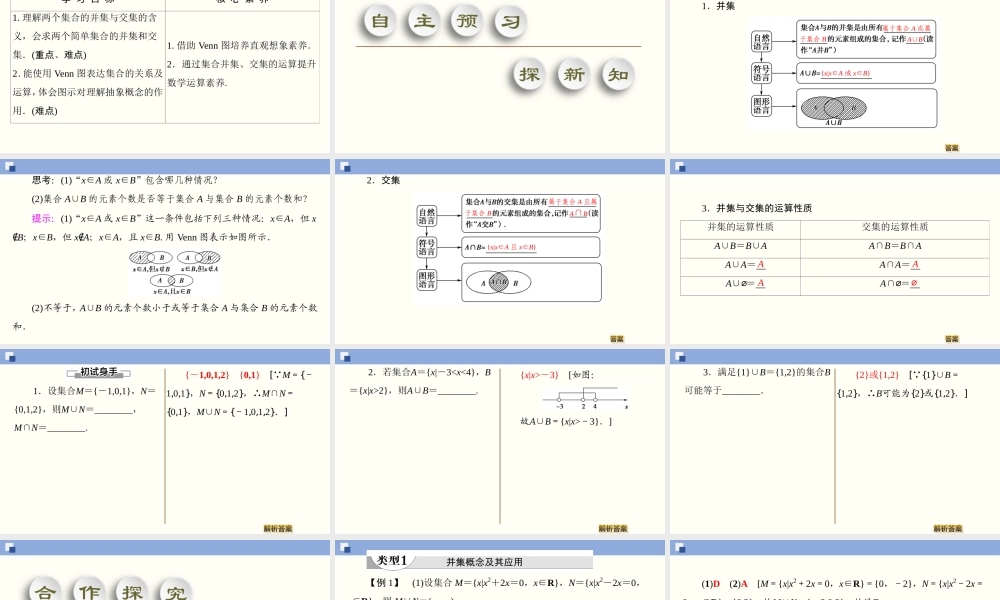
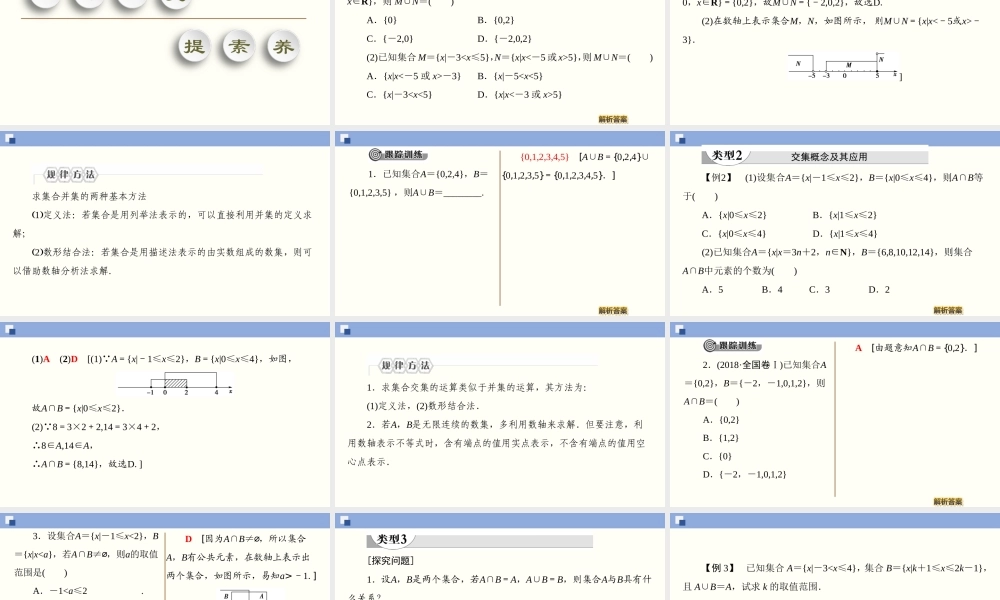
1.3集合的基本运算数学(人教版)第一章集合与常用逻辑用语第1课时并集和交集学习目标核心素养1.理解两个集合的并集与交集的含义,会求两个简单集合的并集和交集.(重点、难点)2.能使用Venn图表达集合的关系及运算,体会图示对理解抽象概念的作用.(难点)1.借助Venn图培养直观想象素养.2.通过集合并集、交集的运算提升数学运算素养.自主预习探新知1.并集属于集合A或属于集合BA∪B{x|x∈A或x∈B}思考:(1)“x∈A或x∈B”包含哪几种情况?(2)集合A∪B的元素个数是否等于集合A与集合B的元素个数和?提示:(1)“x∈A或x∈B”这一条件包括下列三种情况:x∈A,但x∉B;x∈B,但x∉A;x∈A,且x∈B.用Venn图表示如图所示.(2)不等于,A∪B的元素个数小于或等于集合A与集合B的元素个数和.2.交集属于集合A且属于集合BA∩B{x|x∈A且x∈B}3.并集与交集的运算性质并集的运算性质交集的运算性质A∪B=B∪AA∩B=B∩AA∪A=A∩A=A∪∅=A∩∅=AAA∅1.设集合M={-1,0,1},N={0,1,2},则M∪N=________,M∩N=________.{-1,0,1,2}{0,1}[ M={-1,0,1},N={0,1,2},∴M∩N={0,1},M∪N={-1,0,1,2}.]2.若集合A={x|-32},则A∪B=________.{x|x>-3}[如图:故A∪B={x|x>-3}.]3.满足{1}∪B={1,2}的集合B可能等于________.{2}或{1,2}[ {1}∪B={1,2},∴B可能为{2}或{1,2}.]合作探究提素养【例1】(1)设集合M={x|x2+2x=0,x∈R},N={x|x2-2x=0,x∈R},则M∪N=()A.{0}B.{0,2}C.{-2,0}D.{-2,0,2}(2)已知集合M={x|-35},则M∪N=()A.{x|x<-5或x>-3}B.{x|-55}并集概念及其应用(1)D(2)A[M={x|x2+2x=0,x∈R}={0,-2},N={x|x2-2x=0,x∈R}={0,2},故M∪N={-2,0,2},故选D.(2)在数轴上表示集合M,N,如图所示,则M∪N={x|x<-5或x>-3}.]求集合并集的两种基本方法1定义法:若集合是用列举法表示的,可以直接利用并集的定义求解;2数形结合法:若集合是用描述法表示的由实数组成的数集,则可以借助数轴分析法求解.1.已知集合A={0,2,4},B={0,1,2,3,5},则A∪B=________.{0,1,2,3,4,5}[A∪B={0,2,4}∪{0,1,2,3,5}={0,1,2,3,4,5}.]【例2】(1)设集合A={x|-1≤x≤2},B={x|0≤x≤4},则A∩B等于()A.{x|0≤x≤2}B.{x|1≤x≤2}C.{x|0≤x≤4}D.{x|1≤x≤4}(2)已知集合A={x|x=3n+2,n∈N},B={6,8,10,12,14},则...