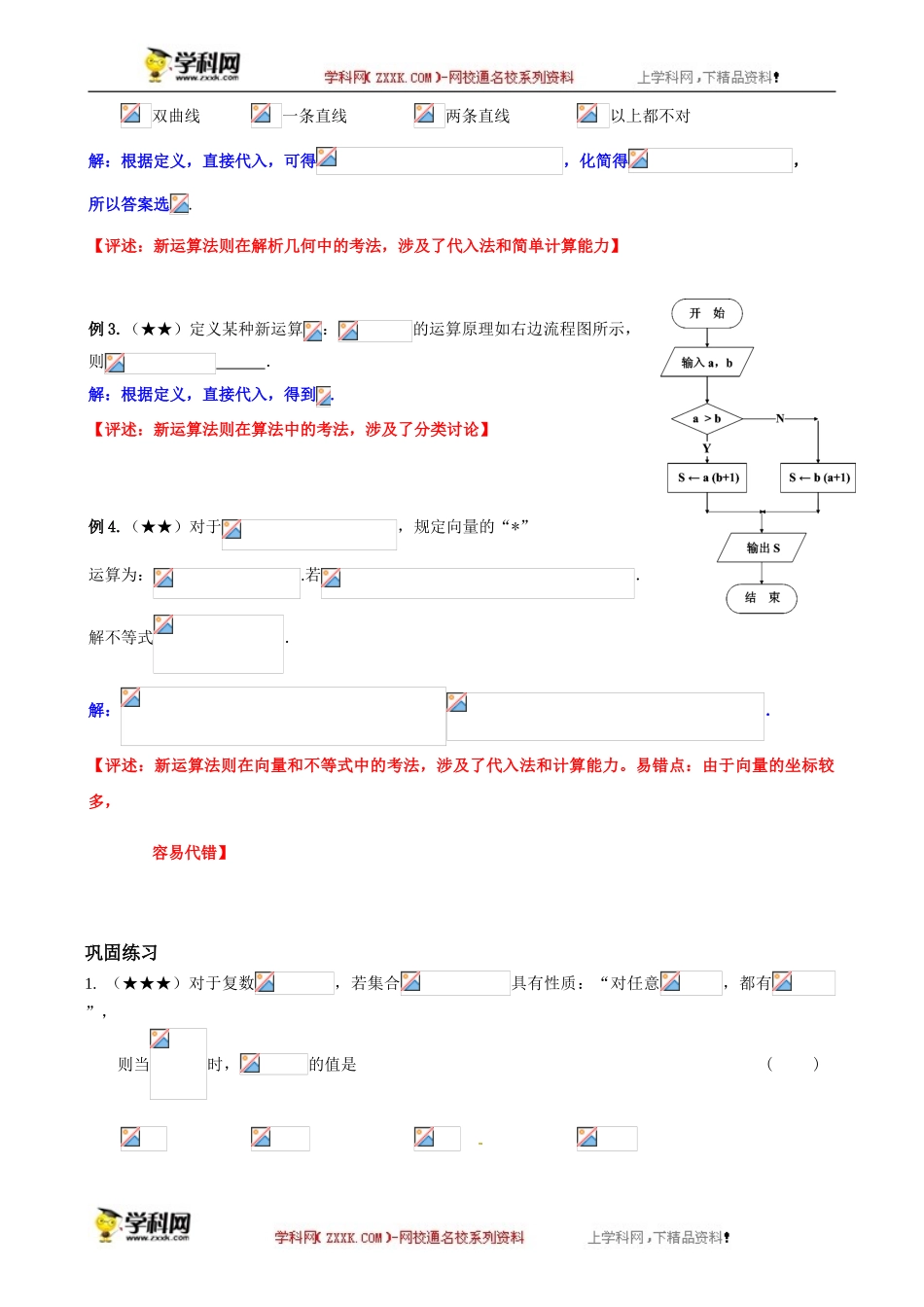
沪教版(上海)高中数学2019-2020学年度高三数学二轮复习专题之新定义题型教学目标了解简单新定义题型的主要命题方式,并掌握最主要的两类的不同做法。【解读:新定义题型变化较多,此专题属于“入门”级别,涉及的章节较多】知识梳理无典例精讲【说明:此部分所给题量较大,大都是高考原题、一二模考题。各位老师可以根据学生的程度、是否做过等因素,自由组合课前作业、课堂例题、课堂练习、课后作业等】类型一:“新运算法则”例1.(★★)定义集合运算:.设,则集合的所有元素之和为.解:根据定义,直接列举法,可得,所以答案是.【评述:新运算法则在集合中的考法,涉及了集合意义的理解、列举法等。易错点:要注意元素的互异性,只有一个,所以不是】例2.(★★)在实数集上定义运算:,则满足的实数对在平面直角坐标系中对应点的轨迹为()双曲线一条直线两条直线以上都不对解:根据定义,直接代入,可得,化简得,所以答案选.【评述:新运算法则在解析几何中的考法,涉及了代入法和简单计算能力】[来源:学。科。网]例3.(★★)定义某种新运算:的运算原理如右边流程图所示,则.解:根据定义,直接代入,得到.【评述:新运算法则在算法中的考法,涉及了分类讨论】例4.(★★)对于,规定向量的“*”运算为:.若.解不等式.解:.【评述:新运算法则在向量和不等式中的考法,涉及了代入法和计算能力。易错点:由于向量的坐标较多,容易代错】[来源:Zxxk.Com]巩固练习1.(★★★)对于复数,若集合具有性质:“对任意,都有”,则当时,的值是()解:直接解方程组,得或,所以,选【评述:新运算法则在集合和复数中的考法,涉及了集合的互异性和复数的计算。难点:对于性质的理解与使用,特别是“任意”两字】2.(★★★)对于直角坐标系内任意两点、,定义运算:,若点的坐标为,且则等于.解:根据定义,代入计算,得,则,所以.【评述:新运算法则在向量中的考法,涉及了简单计算和利用数量积求角】3.(★★★)对于任意的平面向量,定义新运算:.若为平面向量,,则下列运算性质一定成立的所有序号是.①;②;③④;⑤.解:根据定义,直接代入计算,得到正确的是①③【评述:新运算法则在向量中的考法,涉及了简单计算,需要一个一个地验证】4.(★★★)我们知道,当两个矩阵、的行数与列数分别相等时,将它们对应位置上的元素相减,所得到的矩阵称为矩阵与的差,记作.已知矩阵,满足.求下列三角比的值:(1),;(2).解:(1),...