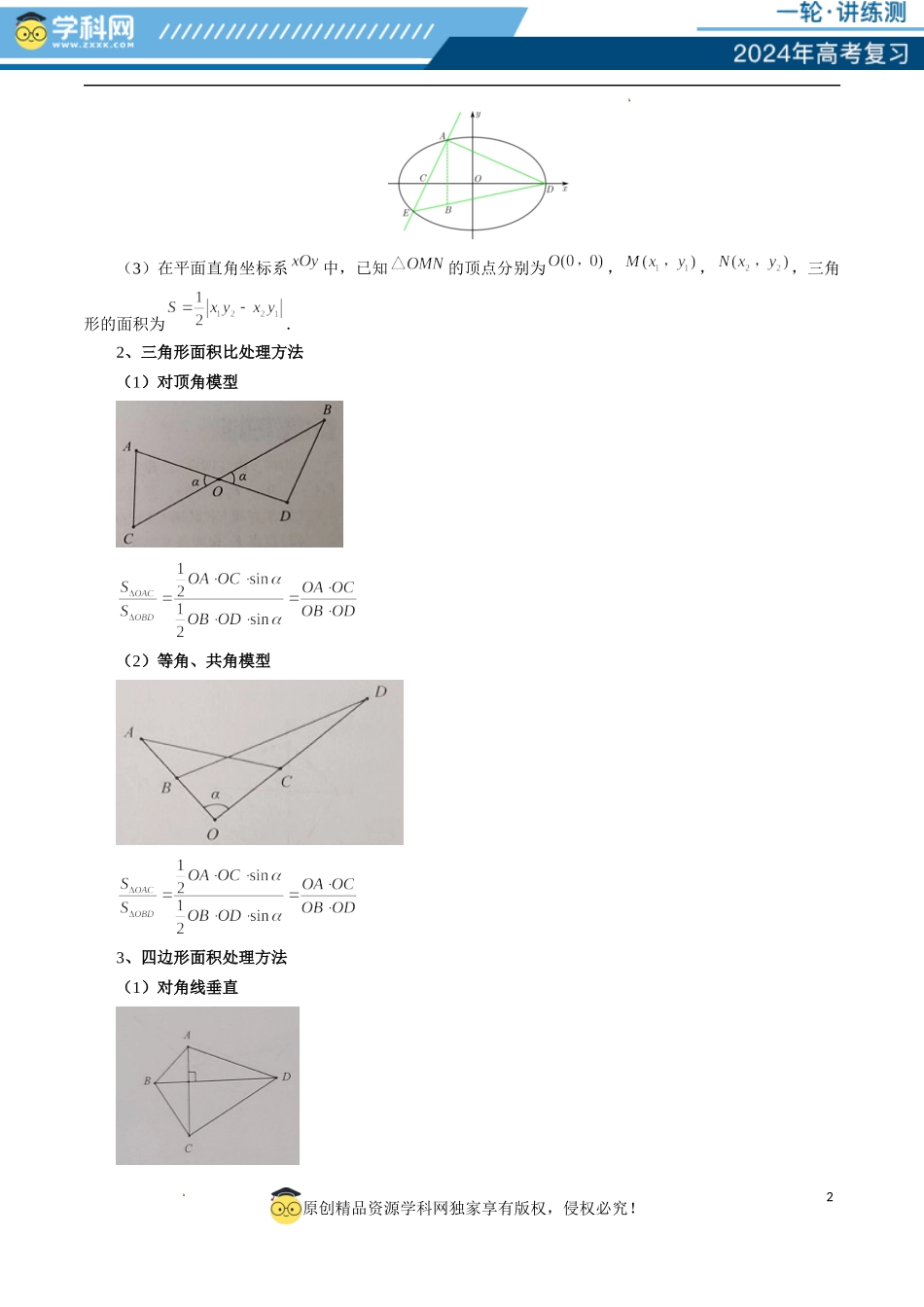
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司重难点突破07圆锥曲线三角形面积与四边形面积题型全归类目录1、三角形的面积处理方法(1)底·高(通常选弦长做底,点到直线的距离为高)(2)水平宽·铅锤高或2原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司(3)在平面直角坐标系中,已知的顶点分别为,,,三角形的面积为.2、三角形面积比处理方法(1)对顶角模型(2)等角、共角模型3、四边形面积处理方法(1)对角线垂直3原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司(2)一般四边形(3)分割两个三角形4、面积的最值问题或者取值范围问题一般都是利用面积公式表示面积,然后将面积转化为某个变量的一个函数,再求解函数的最值(一般处理方法有换元,基本不等式,建立函数模型,利用二次函数、三角函数的有界性求最值或利用导数法求最值,构造函数求导等等),在算面积的过程中,优先选择长度为定值的线段参与运算,灵活使用割补法计算面积,尽可能降低计算量.题型一:三角形的面积问题之底·高例1.(2023·福建漳州·高三统考开学考试)已知椭圆的左焦点为,且过点.(1)求C的方程;(2)不过原点O的直线与C交于P,Q两点,且直线OP,PQ,OQ的斜率成等比数列.(i)求的斜率;(ii)求的面积的取值范围.4原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司【解析】(1)由题知,椭圆C的右焦点为,且过点,所以,所以.又,所以,所以C的方程为.(2)(ⅰ)由题知,直线l的斜率存在,且不为0.设,,,则,所以,所以,,且,即.因为直线OP,PQ,OQ的斜率成等比数列.所以,即,所以,且.因为,所以,所以.(ii)由(ⅰ)知,,所以,且.设点O到直线PQ的距离为d,所以.因为,所以,,5原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司所以,又,且.所以即的面积的取值范围.例2.(2023·湖南常德·高三常德市一中校考阶段练习)在平面直角坐标系中,已知点,点在直线上运动,过点与垂直的直线和的中垂线相交于点.(1)求动点的轨迹的方程;(2)设点是轨迹上的动点,点在轴上,圆内切于,求的面积的最小值.【解析】(1)设点为轨迹上任意一点,由题意知,,所以动点的轨迹是以为焦点,以为...