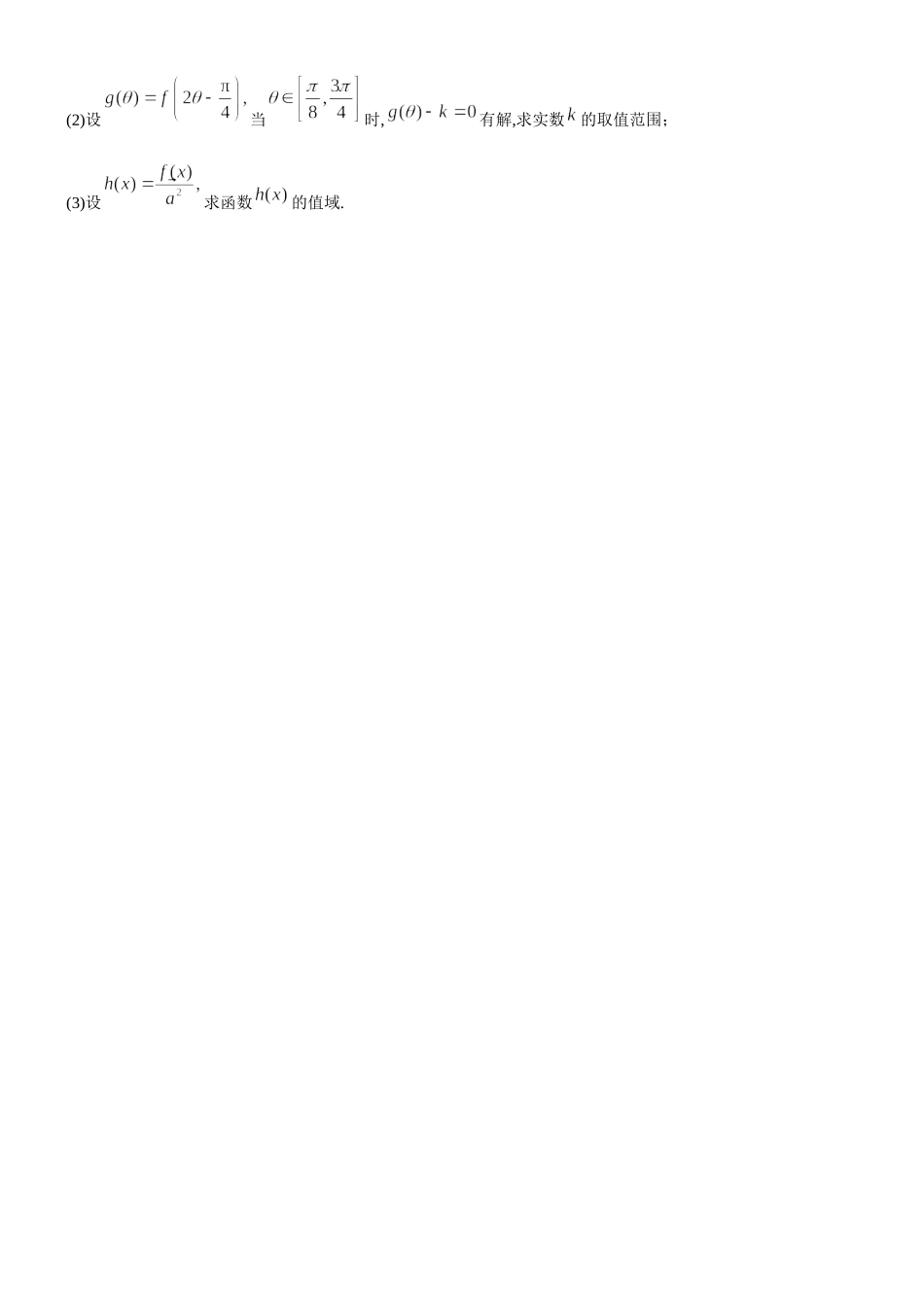
A15.函数综合(1)一、基础知识1.函数是最重要的数学思想,在处理函数综合问题时,借助函数图象数形结合处理函数综合问题是重要且有效的方法.分类讨论、换元、等价转化是常见的处理手段.2.一次、二次、指数、对数、幂函数、双勾、双升、双减、一二次比式、三角函数等是函数的基本载体.二、典型例题与基本方法1.若函数区间上的值域为则的值是2.如果函数且在上是增函数,则实数的取值范围是3.如果函数在区间上单调递减,则的最大值为4.已知函数的图象上关于轴对称的点恰好有3对,则实数的取值范围是5.已知函数定义函数给出下列命题:①;②函数是偶函数;③当时,若则有成立;④当时,函数有4个零点.其中正确结论的序号是6.函数的值域为7.若函数的最大值为11,则8.在中,,点分别在边上,且,则的最大值为9.已知在中,,若为线段上的点,且,则的最大值为10.在扇形中,为弧上的一个动点.若,则的取值范围是11.设.(1)求的值.(2)已知的定义域为求实数的取值范围.12.已知向量函数(1)求函数的解析式;(2)设当时,有解,求实数的取值范围;(3)设求函数的值域.13.已知两点的坐标分别为,其中(1)求的表达式;(2)若为坐标原点),求的值;(3)若,求函数的最小值.B15.练习姓名:1.关于的方程,给出下列四个命题:①存在实数,使得方程恰有2个不同的实根;②存在实数,使得方程恰有4个不同的实根;③存在实数,使得方程恰有5个不同的实根;④存在实数,使得方程恰有8个不同的实根.其中假命题的个数是()A.0B.1C.2D.32.在中,角的对边分别是,若,则的大小为3.设为锐角,若,则的值为4.若方程有两个不同的解,则实数的取值范围是5.已知函数的值域为,设,若不等式在上有解,则实数的取值范围为6.如图,矩形中,分别为线段的点,且满足,若,则的最小值为7.已知向量(1)求的值;(2)若,且,求的值.8.已知向量及实数满足若且(1)求关于的函数关系式及其定义域;(2)若时,不等式恒成立,求实数的取值范围.A15.函数综合(1)一、基础知识1.函数是最重要的数学思想,在处理函数综合问题时,借助函数图象数形结合处理函数综合问题是重要且有效的方法.分类讨论、换元、等价转化是常见的处理手段.2.一次、二次、指数、对数、幂函数、双勾、双升、双减、一二次比式、三角函数等是函数的基本载体.二、典型例题与基本方法1.若函数区间上的值域为则的值是解:由为奇函数,所以函数的图象关于对称.因为函数的值域为所以于是2.如果函数且在上是增函数,则实数的取值范围是解:令则当时,函数在上单调递增,且要使原函数是增函数,二次函数需要...