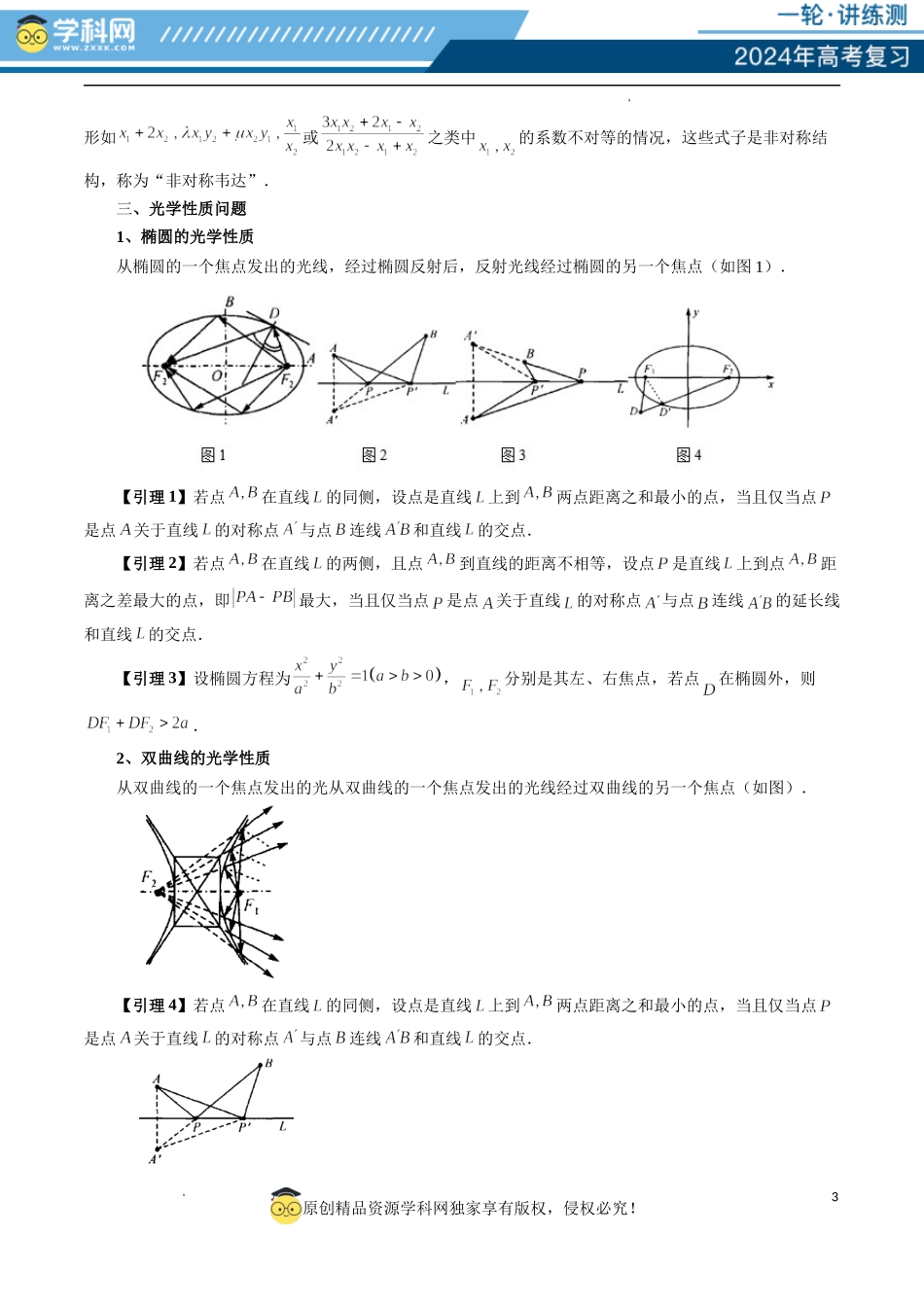
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司重难点突破19圆锥曲线中的仿射变换、非对称韦达、光学性质、三点共线问题目录一、仿射变换问题仿射变换有如下性质:1、同素性:在经过变换之后,点仍然是点,线仍然是线;2、结合性:在经过变换之后,在直线上的点仍然在直线上;3、其它不变关系.我们以椭圆为例阐述上述性质.椭圆,经过仿射变换,则椭圆变为了圆,并且变换过程有如下对应关系:(1)点变为;2原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司(2)直线斜率变为,对应直线的斜率比不变;(3)图形面积变为,对应图形面积比不变;(4)点、线、面位置不变(平⾏直线还是平⾏直线,相交直线还是相交直线,中点依然是中点,相切依然是相切等);(5)弦长关系满足,因此同一条直线上线段比值不变,三点共线的比不变总结可得下表:变换前变换后方程横坐标纵坐标斜率面积弦长不变量平行关系;共线线段比例关系;点分线段的比二、非对称韦达问题在一元二次方程中,若,设它的两个根分别为,则有根与系数关系:,借此我们往往能够利用韦达定理来快速处理之类的结构,但在有些问题时,我们会遇到涉及的不同系数的代数式的应算,比如求或之类的结构,就相对较难地转化到应用韦达定理来处理了.特别是在圆锥曲线问题中,我们联立直线和圆锥曲线方程,消去或,也得到一个一元二次方程,我们就会面临着同样的困难,我们把这种3原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司形如或之类中的系数不对等的情况,这些式子是非对称结构,称为“非对称韦达”.三、光学性质问题1、椭圆的光学性质从椭圆的一个焦点发出的光线,经过椭圆反射后,反射光线经过椭圆的另一个焦点(如图1).【引理1】若点在直线的同侧,设点是直线上到两点距离之和最小的点,当且仅当点是点关于直线的对称点与点连线和直线的交点.【引理2】若点在直线的两侧,且点到直线的距离不相等,设点是直线上到点距离之差最大的点,即最大,当且仅当点是点关于直线的对称点与点连线的延长线和直线的交点.【引理3】设椭圆方程为,分别是其左、右焦点,若点在椭圆外,则.2、双曲线的光学性质从双曲线的一个焦点发出的光从双曲线的一个焦点发出的光线经过双曲线的另一个焦点(如图).【引理4】若点在直线的同侧,设点是直线...