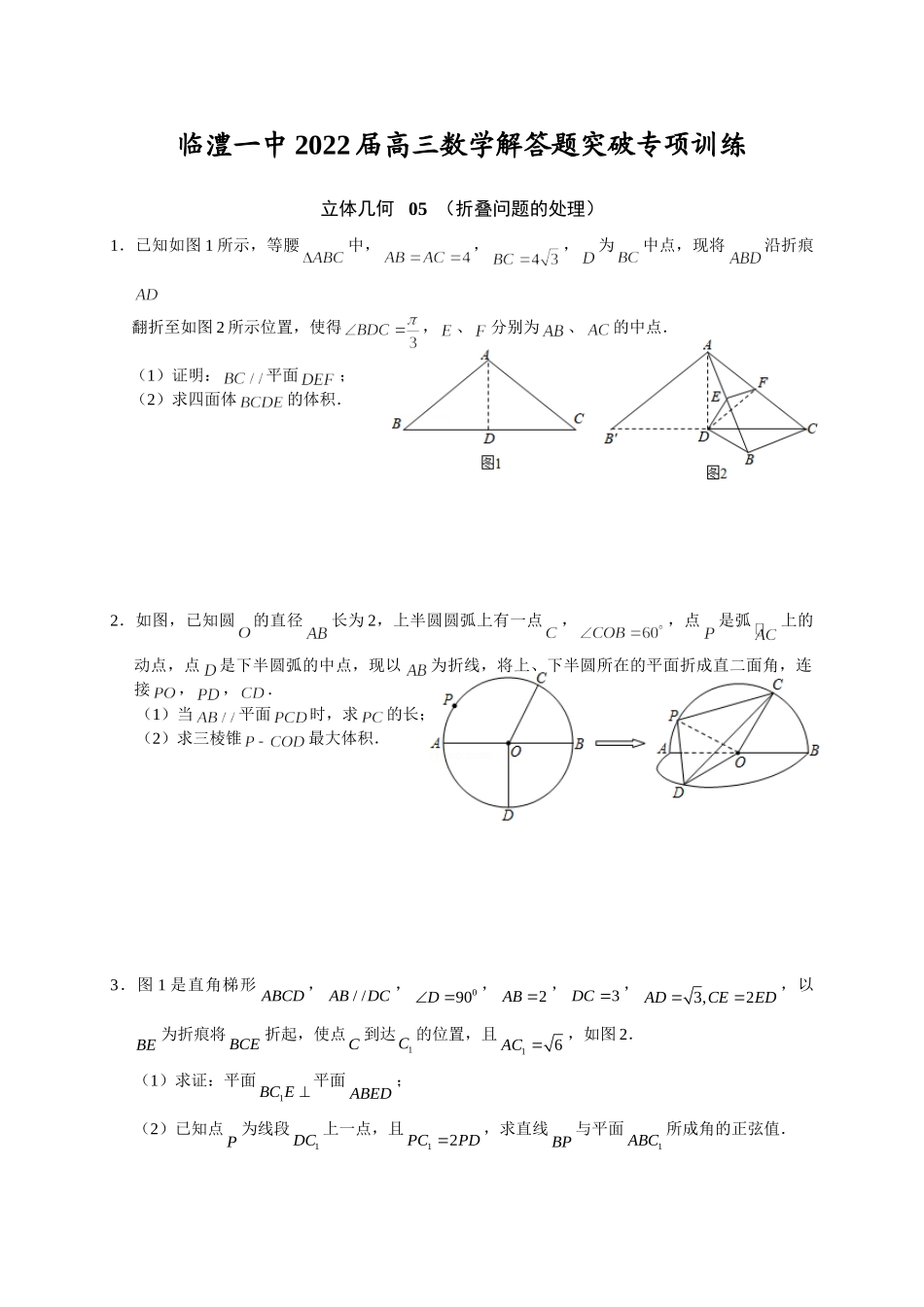
临澧一中2022届高三数学解答题突破专项训练立体几何05(折叠问题的处理)1.已知如图1所示,等腰中,,,为中点,现将沿折痕翻折至如图2所示位置,使得,、分别为、的中点.(1)证明:平面;(2)求四面体的体积.2.如图,已知圆的直径长为2,上半圆圆弧上有一点,,点是弧上的动点,点是下半圆弧的中点,现以为折线,将上、下半圆所在的平面折成直二面角,连接,,.(1)当平面时,求的长;(2)求三棱锥最大体积.3.图1是直角梯形ABCD,//ABDC,090D,2AB,3DC,3,2ADCEED�,以BE为折痕将BCE折起,使点C到达1C的位置,且16AC,如图2.(1)求证:平面1BCE平面ABED;(2)已知点P为线段1DC上一点,且12PCPD,求直线BP与平面1ABC所成角的正弦值.4.如图,在平行四边形ABCD中,60D,E为CD的中点,且AECE,现将平行四边形沿AE折叠成四棱锥PABCE.(1)已知M为AB的中点,求证:AEPM;(2)若平面PAE平面ACBE,求二面角BPEC的余弦值.5.如图①所示,平面五边形ABCDE中,四边形ABCD为直角梯形,90B且//ADBC,若22ADBC,3AB,ADE是以AD为斜边的等腰直角三角形,现将ADE沿AD折起,连接EB,EC得如图②的几何体.(1)若点M是ED的中点,求证://CM平面ABE;(2)若2EC,在棱EB上是否存在点F,使得二面角EADF的大小为60?若存在,求出点F的位置;若不存在,请说明理由.6.图(1)是由矩形ADEB,RtABC和菱形BFGC组成的一个平面图形,其中1AB,2BEBF,60FBC,将其沿AB,BC折起使得BE,BF重合,连接DG,如图(2).(1)证明图(2)中A,C,G,D四点共面;(2)求图(2)中二面角BADC的大小.7.如图(1)在直角梯形ABCD中,//ADBC,90CDA,2AD,1BCCD,BEAD,沿BE将ABE折起得到四棱锥ABCDE,如图(2)所示.(1)证明:平面AED平面BCDE;(2)若二面角ABED的大小为60,M,N分别是AD,DE的中点.(ⅰ)求CN与平面ACD所成角的正弦值;(ⅱ)在棱AC上是否存在点G,使得//DG平面BMN?若存在,求出:AGGC的值;若不存在,说明理由.8.如图(1),在四棱锥和四面体中,四边形为矩形,两个和△全等,△为等边三角形,且,棱锥的四条侧棱相等,平面.现将两个几何体中的和△重合,构成一个新的几何体,如图(2),并且.(1)证明:点为两个平面和平面的一个公共点;(2)求平面与平面所成角(锐角)的余弦值.参考答案1.(1)证明:、分别为、的中...