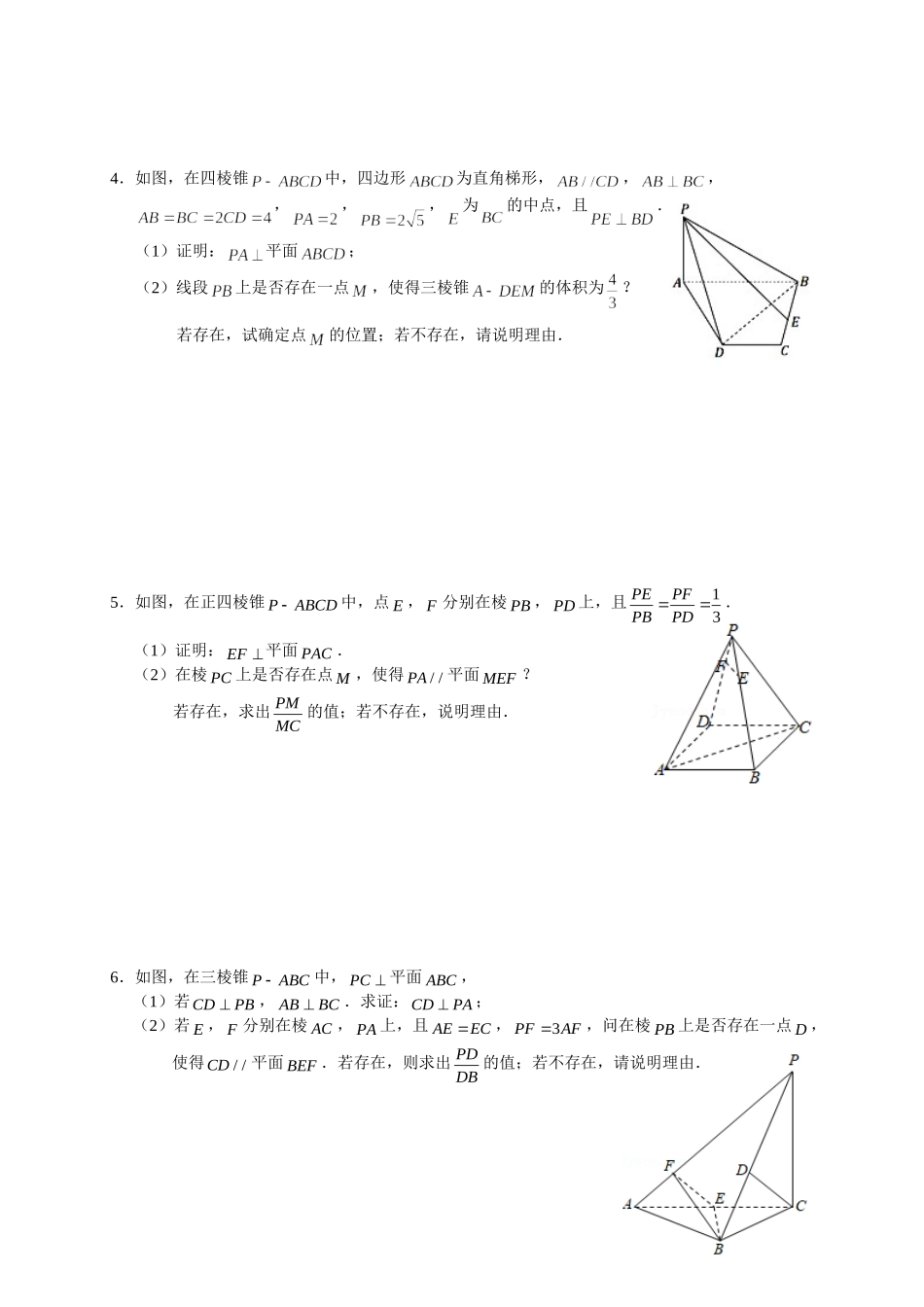
临澧一中2022届高三数学解答题突破专项训练立体几何04(探索性问题的处理)1.如图所示,在三棱柱中,平面平面,,,,分别为,的中点,且.(1)在棱上是否存在点,使得平面?若存在,请找出点的位置;若不存在,请说明理由;(2)求三棱锥的体积.2.如图,在底面是菱形的四棱锥中,60ABC,PAACa,2PBPDa,点E在PD上,且:3:1PEED.(1)证明:PA平面ABCD;(2)在棱PC上是否存在一点F,使//BF平面AEC?证明你的结论.3.如图,在三棱锥中,,,平面平面.(1)求证:;(2)已知,,则棱上是否存在点,使得平面平面?若存在,确定点的位置;若不存在,请说明理由.4.如图,在四棱锥中,四边形为直角梯形,,,,,,为的中点,且.(1)证明:平面;(2)线段上是否存在一点,使得三棱锥的体积为?若存在,试确定点的位置;若不存在,请说明理由.5.如图,在正四棱锥PABCD中,点E,F分别在棱PB,PD上,且13PEPFPBPD.(1)证明:EF平面PAC.(2)在棱PC上是否存在点M,使得//PA平面MEF?若存在,求出PMMC的值;若不存在,说明理由.6.如图,在三棱锥PABC中,PC平面ABC,(1)若CDPB,ABBC.求证:CDPA;(2)若E,F分别在棱AC,PA上,且AEEC,3PFAF,问在棱PB上是否存在一点D,使得//CD平面BEF.若存在,则求出PDDB的值;若不存在,请说明理由.7.如图,在四棱锥PABCD中,底面ABCD为平行四边形,O,M分别为BD,PC的中点.设平面PAD与平面PBC的交线为l.(1)求证://OM平面PAD;(2)求证://BCl;(3)在棱PC上是否存在点N(异于点)C,使得//BN平面PAD?若存在,求出PNPC的值;若不存在,说明理由.8.如图,在四棱锥PABCD中,四边形ABCD为直角梯形,//ABCD,ABBC,24ABBCCD,2PA,25PB,E为BC的中点,且PEBD.(1)证明:PA平面ABCD;(2)线段PB上是否存在一点M,使得二面角MDEA的余弦值为539?若存在,试确定点M的位置;若不存在,请说明理由.9.如图,点O是正方形ABCD两对角线的交点,DE平面ABCD,BF平面ABCD,2ABBFDE,M是线段EF上点,且2MFME.(1)证明:三棱锥MACF是正三棱锥;(2)试问在线段DF(不含端点)上是否存在一点N,使得//CN平面ABF.若存在,请指出点N的位置;若不存在,请说明理由.参考答案1.(1)存在,当点与点重合时平面.证明如下:连接,,分别为,的中点,,且,可得四边形为平行四边形,则,平面,平面,平面,即平面;(2)平...