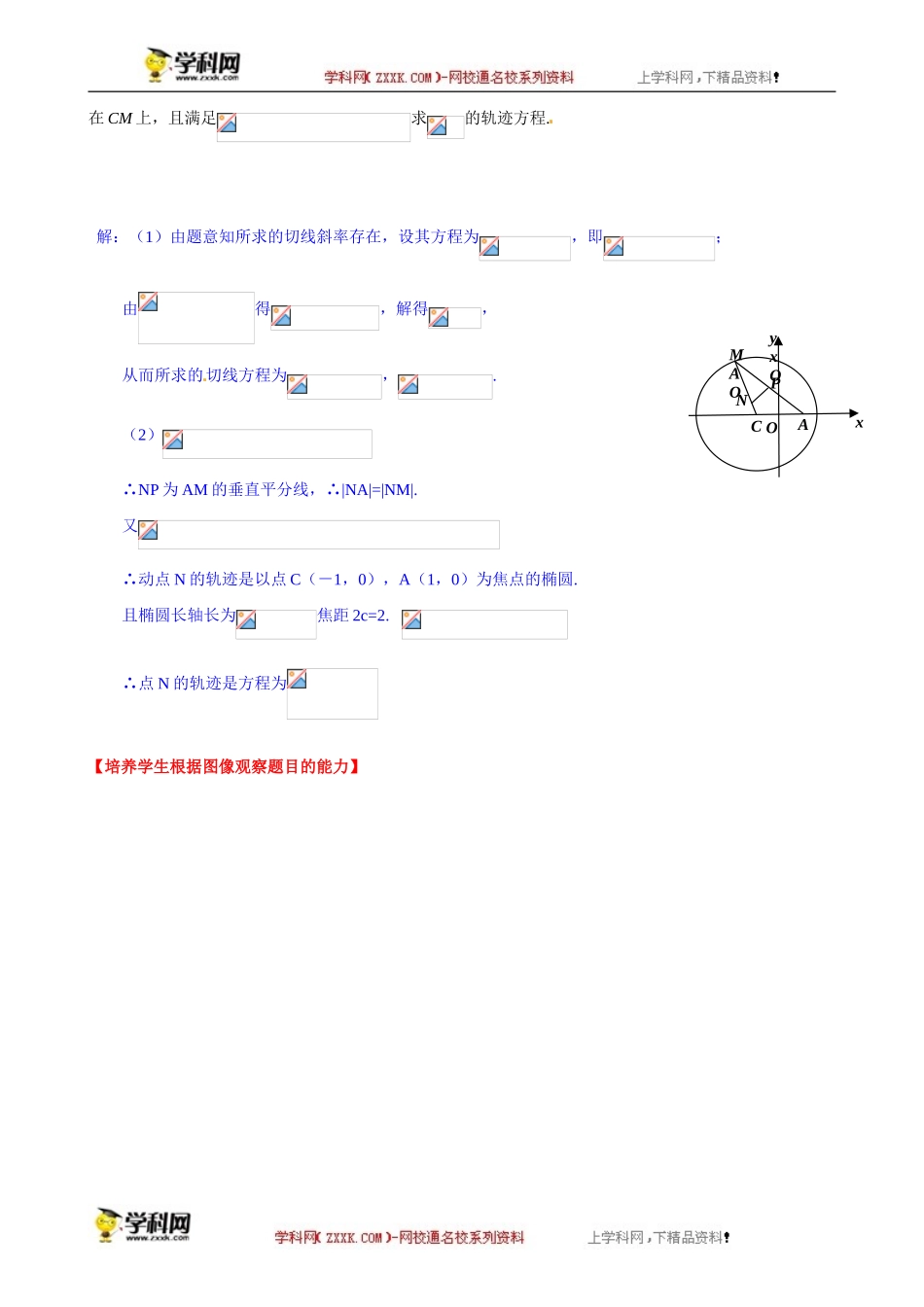
沪教版(上海)高中数学2019-2020学年度高三数学二轮复习向量专题之向量语言的转化教学目标1、向量语言向代数语言的转化;2、掌握一些特殊向量表达式的意义;知识梳理(1)给出与相交,等于已知过的中点;(2)给出,等于已知是的中点;(3)给出,等于已知,与的中点三点共线;(4)给出以下情形之一:①;②存在实数,使;③若存在实数,,且,使,等于已知,,三点共线.(5)给出,等于已知是的定比分点,为定比,即;(6)给出,等于已知是的平分线;(7)在平行四边形中,给出,等于已知是菱形;(8)在平行四边形中,给出,等于已知是矩形;(9)在中,给出,等于已知是的外心(三角形外接圆的圆心,三角形的外心是三角形三边垂直平分线的交点);(10)在中,给出,等于已知是的重心(三角形的重心是三角形三条中线的交点);(11)在中,给出,等于已知是的垂心(三角形的垂心是三角形三条高的交点);(12)在中,给出等于已知通过的内心;(13)在中,给出等于已知是的内心(三角形内切圆的圆心,三角形的内心是三角形三条角平分线的交点);[来源:学+科+网](14)在中,给出,等于已知是中边的中线.【在讲解的过程中注意画图,帮助理解】典例精讲(模板一)例1.(★★)点O在所在平面内,给出下列关系式:(1);(2);(3);(4).则点O依次为的(C).内心、外心、重心、垂心;.重心、外心、内心、垂心;.重心、垂心、内心、外心;.外心、内心、垂心、重心.【讲解的完了之后注意让学生自己把上面的结论记住】[来源:Zxxk.Com]巩固练习1.(★)若有不同的三点满足则这三点[答](C)A.组成锐角三角形B.组成直角三角形C.组成钝角三角形D.在同一条直线例2.(★★)已知圆.(1)求过点的圆C的切线的方程;(2)如图,为圆C上一动点,点P在AM上,点NxOAMAONCPyxO在CM上,且满足求的轨迹方程.解:(1)由题意知所求的切线斜率存在,设其方程为,即;由得,解得,从而所求的切线方程为,.(2)∴NP为AM的垂直平分线,∴|NA|=|NM|.又∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆.且椭圆长轴长为焦距2c=2.∴点N的轨迹是方程为【培养学生根据图像观察题目的能力】[来源:Z*xx*k.Com][来源:学.科.网]xOAMAONCPyxO例3.(★★★)如图,已知点,直线,为平面上的动点,过作直线的垂线,垂足为点,且.(1)求动点的轨迹的方程;(2)过点的直线交轨迹于两点,交直线于点.1)已知,,求的值;2)求的最小值.解法一:(Ⅰ)设...