解三角形 05 多边多角（多三角形）问题 突破专项训练-2022届高三数学解答题.docVIP免费

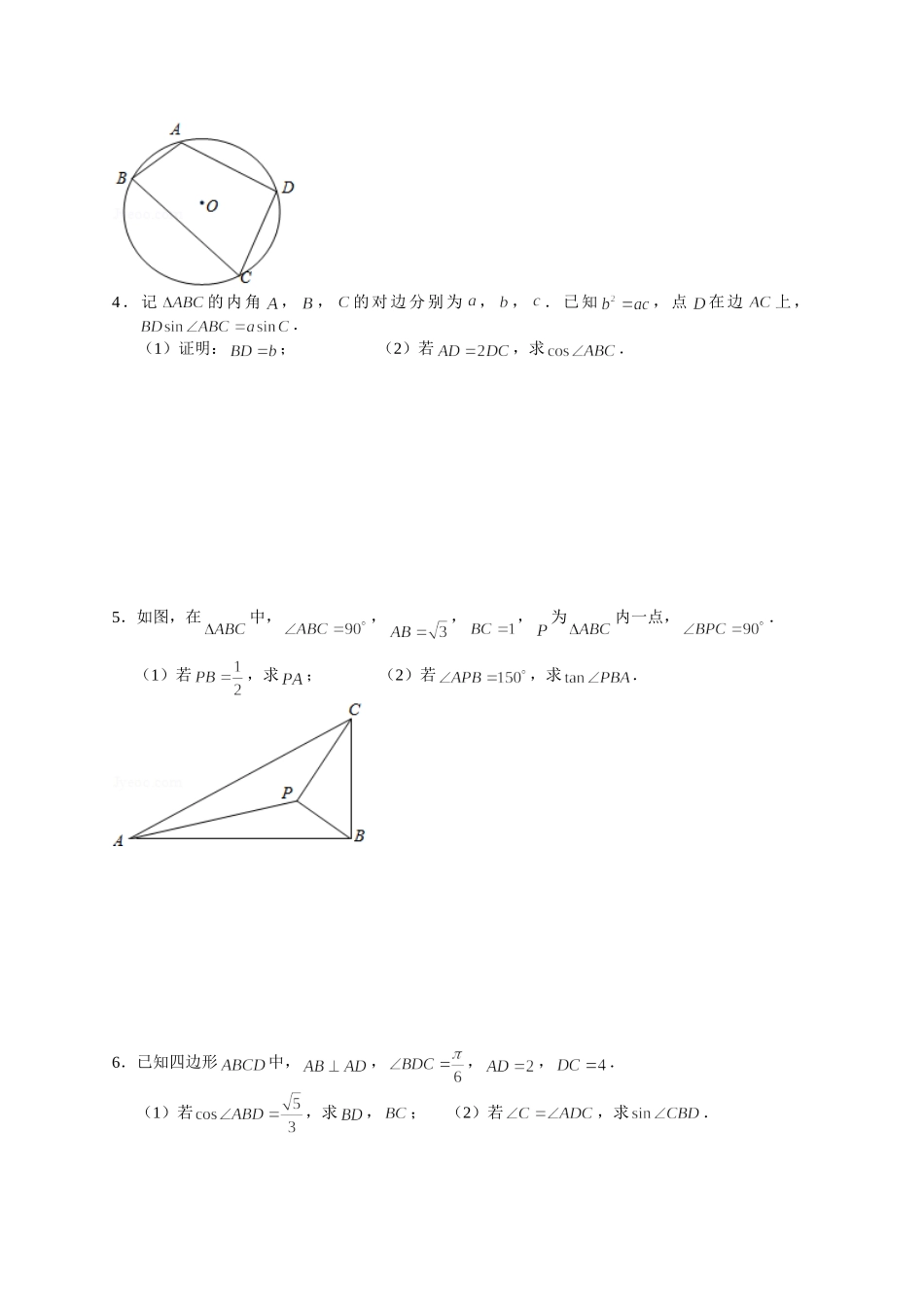
临澧一中2022届高三数学解答题突破专项训练解三角形05（多边多角（多三角形）问题）1．如图，在四边形中，，，．（1）求；（2）若，求周长的最大值．2．△ABC的内角A，B，C所对边分别为a，b，c，已知△ABC的面积为，，，且．（1）求边b；（2）如图，延长BC至点D，使，连接AD，点E为线段AD中点，求．3．如图，（1）在圆的内接四边形中，，，，求的值；（2）在圆的内接四边形中，，，的面积为，求的值．4．记的内角，，的对边分别为，，．已知，点在边上，．（1）证明：；（2）若，求．5．如图，在中，，，，为内一点，．（1）若，求；（2）若，求．6．已知四边形中，，，，．（1）若，求，；（2）若，求．7．在中，内角，，的对边分别为，，，且，．（1）求；（2）如图，圆是的外接圆，延长交于点，过圆心作交于点，且，求的长．8．已知的三个内角，，对应的边分别为，，，．（1）求角的大小；（2）如图，为内一点，，，且，求的最大值．9．如图，，，，为平面四边形的四个内角．（1）证明：；（2）已知，，，，①若，求的值；②求四边形面积的最大值．参考答案1．（1）在中，，所以，利用正弦定理得，所以，又因为为钝角，所以为锐角，故；（2）在中，由余弦定理得，解得或（舍去），在中，，设，，由余弦定理得，即，整理得，又，，利用基本不等式得，即，当且仅当时，等号成立，所以的最大值为8，所以的最大值为，所以周长的最大值为12．2．（1）1233sin21bcAbcSABC…①由余弦定理，25cos222222cbAbccba…②联立①②可得34cb或43cb又cb三角形中，，4b（2）E为AD中点，ACEDCESS，故ACEACECDCEDCECsin21sin21即2sinsinDCACACEDCE3．（1）连接，则中，由余弦定理得，中，由余弦定理得，由圆内接四边形性质可知，，所以，解得；（2）因为，，所以，，由题意，，由余弦定理得，所以，因为，所以，所以，所以．4．（1）证明：由正弦定理知，，，，，，即，．；（2）由（1）知，，，，在中，由余弦定理知，，在中，由余弦定理知，，，，即，得，，，或，在中，由余弦定理知，，当时，（舍；当时，；综上所述，．5．（1）在中，，，．在中，由余弦定理得．．（2）设，在中，．在中，由正弦定理得，即，化为．．6．（1）在中，由于，所以，故，在中，利用余弦定理：，故．（2）设，由于，由，所以，，在中，由于，所以，在中，由正弦定理：，整理得，所以，所以，由于，得...