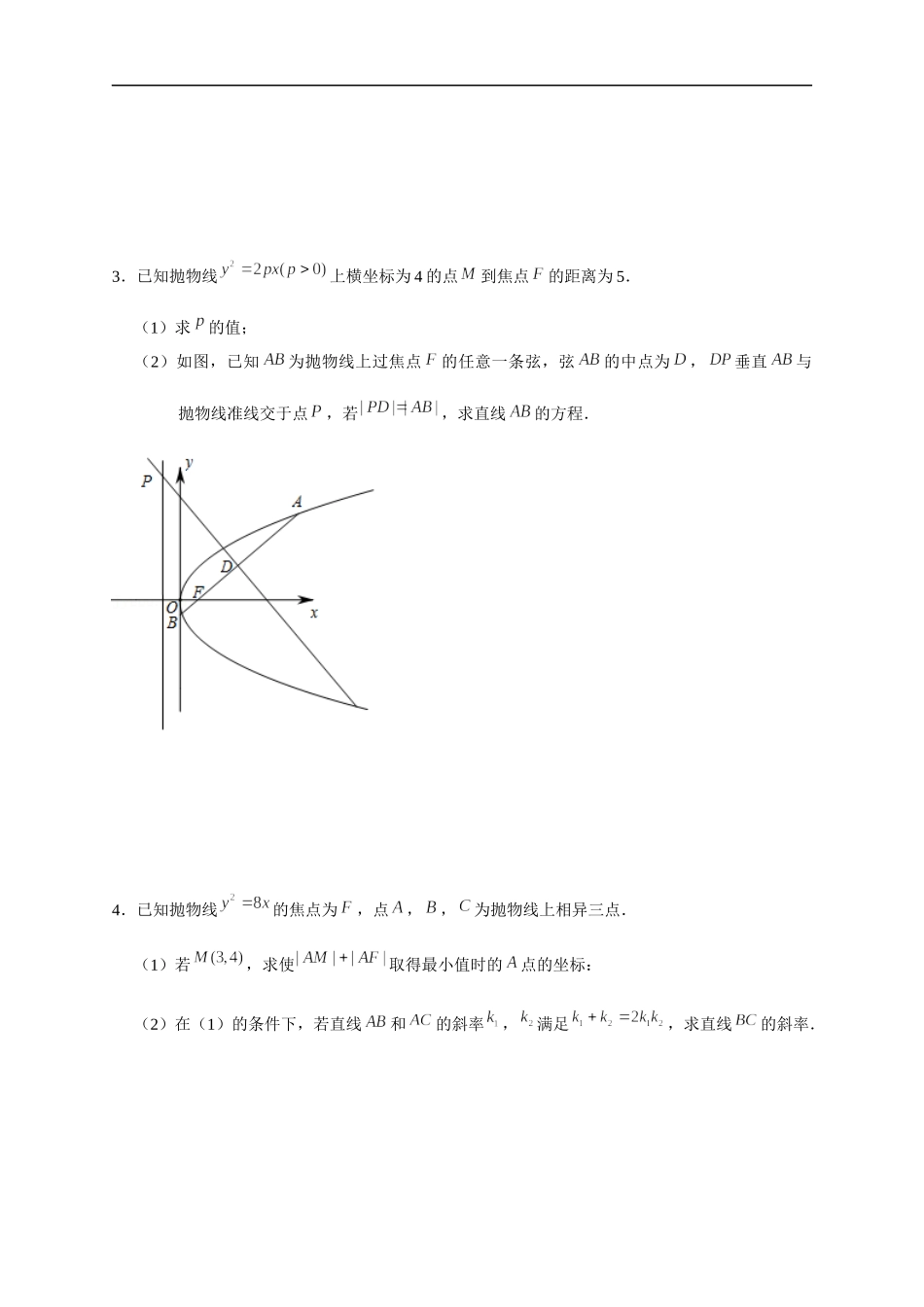
临澧一中2022届高三数学解答题突破专项训练解析几何08(求值、求点、求线问题)1.已知抛物线的焦点为,点在抛物线上,且的面积为为坐标原点).(1)求抛物线的方程;(2)直线与抛物线交于,两点,若以为直径的圆经过点,求直线的方程.2.在平面直角坐标系中,已知双曲线的左顶点为,右焦点为;点在双曲线上,直线与双曲线交于,两点,且当直线的斜率为时,.(1)求双曲线的方程;(2)若,求到直线的距离.3.已知抛物线上横坐标为4的点到焦点的距离为5.(1)求的值;(2)如图,已知为抛物线上过焦点的任意一条弦,弦的中点为,垂直与抛物线准线交于点,若,求直线的方程.4.已知抛物线的焦点为,点,,为抛物线上相异三点.(1)若,求使取得最小值时的点的坐标:(2)在(1)的条件下,若直线和的斜率,满足,求直线的斜率.5.已知椭圆的焦距为2,点在椭圆上.(1)求椭圆的方程;(2)已知直线与椭圆相切于点,与抛物线的准线相交于点,若点为平面内一点,且,求点的坐标.6.已知椭圆其左、右焦点分别为、,且离心率为,点为椭圆的一个顶点,三角形的面积为2.(1)求椭圆的方程;(2)若点为椭圆的左顶点,点在椭圆上,线段的垂直平分线与轴相交于点,若2222:1(0)xyCabab1F2F22B12BFFCAPCAPyQ为等边三角形,求点的横坐标.7.已知椭圆经过点,过右焦点且与轴垂直的直线被截得的线段长为3.(1)求椭圆的方程;(2)点在椭圆上,直线与交于点,过点作的垂线,与轴交于点,若,求点的坐标.8.已知双曲线的一个焦点为,且经过点.(1)求双曲线的标准方程;PAQP2222:1(0)xyCabab(2,0)AFxlCCPCAPlMMAPyQPFQFP(2)已知点是上一定点,过点的动直线与双曲线交于,两点,若为定值,求点的坐标及实数的值.9.已知圆,点是圆上的动点,过点作轴的垂线,垂足为.(1)若点满足,求点的轨迹方程;(2)若过点且斜率分别为,的两条直线与(1)中的轨迹分别交于点、,、,并满足,求的值.10.在平面直角坐标系中,已知双曲线的右焦点为,且经过点,.(1)求双曲线的标准方程;(2)已知,是双曲线上关于原点对称的两点,垂直于的直线与双曲线有且仅有一个公共点,当点位于第一象限,且被轴分割为面积比为的两部分时,求直线的方程.参考答案1.(1)由题意可得,解得.故抛物线的方程为.(2)设,,,.联立,整理得.由直线和抛物线交于、两点可知,且,.依题意,所以,则,即,整理得,解得.故直线的方程为.2.(1...