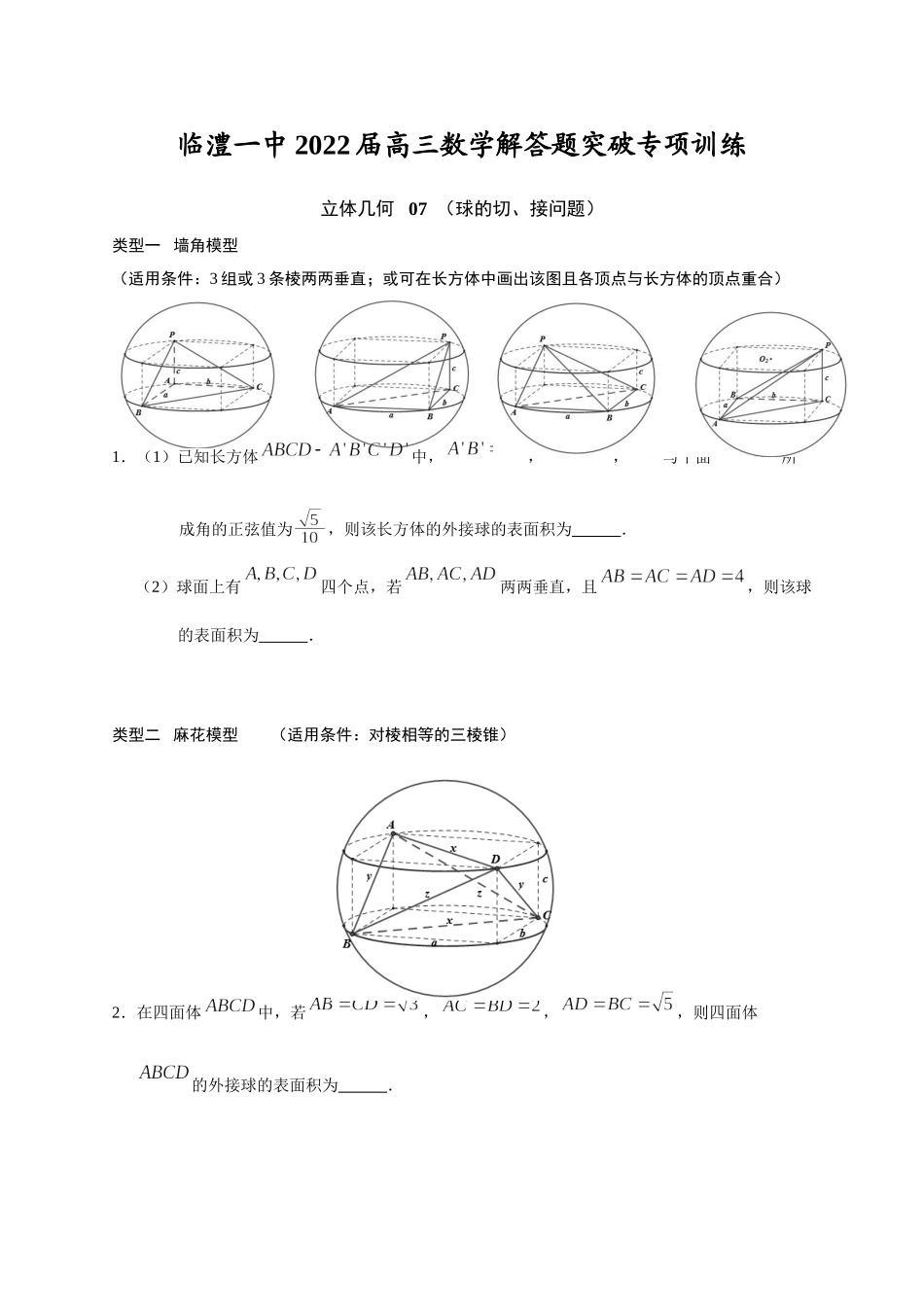
临澧一中2022届高三数学解答题突破专项训练立体几何07(球的切、接问题)类型一墙角模型(适用条件:3组或3条棱两两垂直;或可在长方体中画出该图且各顶点与长方体的顶点重合)1.(1)已知长方体中,,,与平面所成角的正弦值为,则该长方体的外接球的表面积为.(2)球面上有四个点,若两两垂直,且,则该球的表面积为.类型二麻花模型(适用条件:对棱相等的三棱锥)2.在四面体中,若,,,则四面体的外接球的表面积为.类型三矩形模型(适用条件:棱锥有两个平面为直角三角形且斜边为同一边)3.(1)在四面体中,,,则四面体的外接球的表面积为()(2)四面体中,,平面,,,,则该四面体外接球的表面积为()类型四汉堡模型(适用条件:有一条侧棱垂直与底面的柱体或椎体)4.(1)在四棱锥中,四边形是边长为2的正方形,且平面,则该四棱锥外接球的表面积为()(2)如图,在三棱锥A﹣BCD中,BD平面ADC,BD=1,AB=2,BC=3,AC=,则三棱锥A﹣BCD外接球的体积为()(3)三棱柱中,平面,,,,,则该三棱柱的外接球的体积为()(4)在长方体中,,,点在正方形内,平面,则三棱锥的外接球表面积为()类型五折叠模型(适用条件:两个全等三角形或等腰三角形拼在一起,或菱形折叠)5.(1)三棱锥S一ABC中,ABC与SBC都是边长为1的正三角形,二面角A﹣BC﹣S的大小为,若S,A,B,C四点都在球O的表面上,则球O的表面积为()(2)已知二面角的大小为120°,且,,.若点P、A、B、C都在同一个球面上,则该球的表面积的最小值为______.类型六斗笠模型(适用条件:正棱锥或顶点的投影在底面的外心上)6.(1)正三棱锥中,,,则该棱锥外接球的表面积为()(2)已知正三棱锥的侧棱长为,底面边长为6,则该正三棱锥外接球的表面积是________.类型七切瓜模型(适用条件:有两个平面互相垂直的棱锥)7.(1)已知三棱锥中,,,,,面面ABC,则此三棱锥的外接球的表面积为()(2)已知三棱锥中,平面平面,且和都是边长为2的等边三角形,则该三棱锥的外接球表面积为()类型八鳄鱼模型(适用条件:适用所有的棱锥)8.(1)在三棱锥中,和均为边长为2的等边三角形,且二面角的平面角为,则三棱锥的外接球的表面积为________.(2)在三棱锥S-ABC中,AB⊥BC,AB=BC=,SA=SC=2,二面角S-AC-B的余弦值是-,若S,A,B,C都在同一球面上,则该球的表面积是________.(3)已知空间四边形中,,,,若二面角的取值范围为,,则该几何体的外...