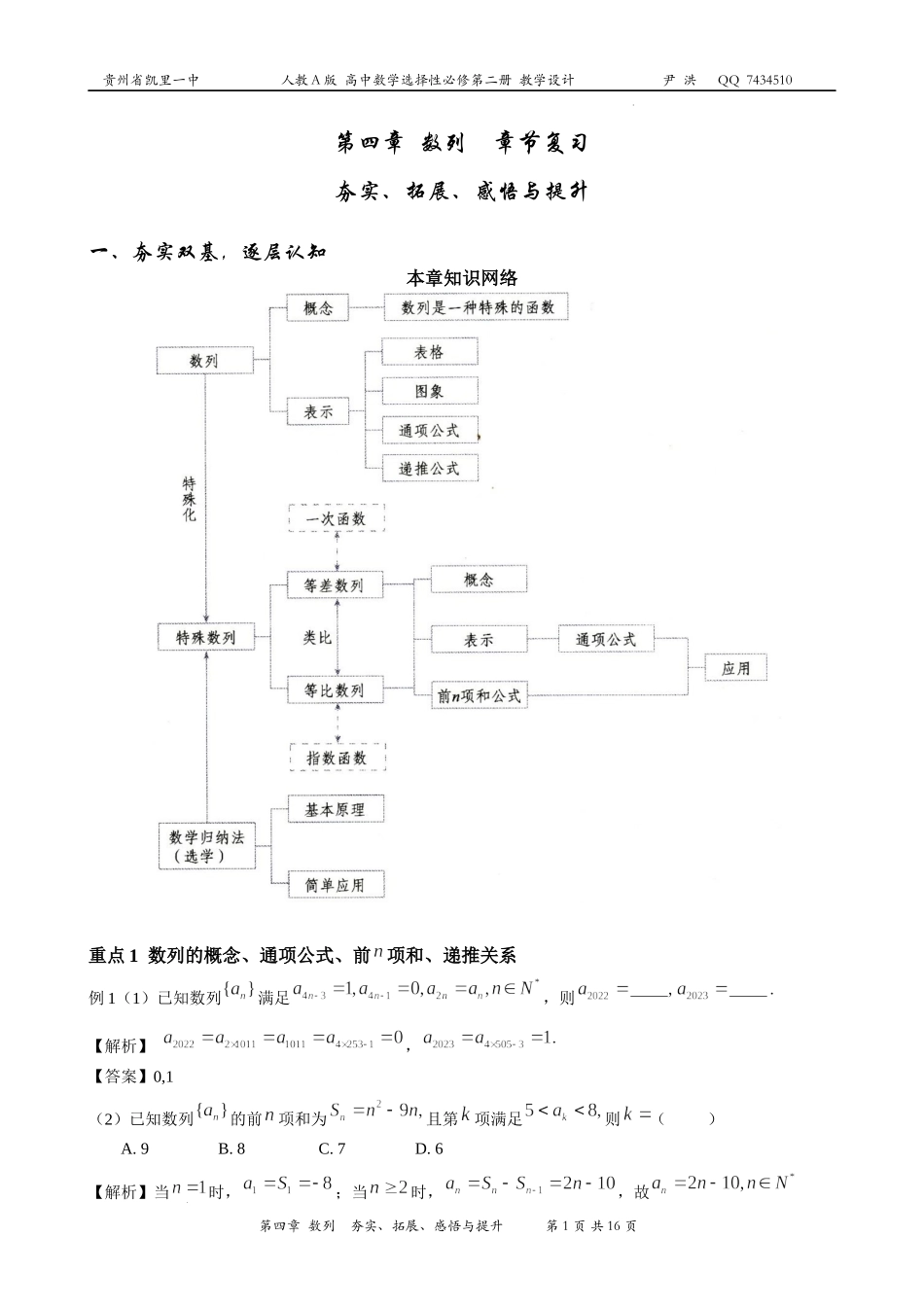
贵州省凯里一中人教A版高中数学选择性必修第二册教学设计尹洪QQ7434510第四章数列夯实、拓展、感悟与提升第1页共16页学科网(北京)股份有限公司第四章数列章节复习夯实、拓展、感悟与提升一、夯实双基,逐层认知本章知识网络重点1数列的概念、通项公式、前项和、递推关系例1(1)已知数列满足,则【解析】,【答案】0,1(2)已知数列的前项和为且第项满足则()A.9B.8C.7D.6【解析】当时,;当时,,故贵州省凯里一中人教A版高中数学选择性必修第二册教学设计尹洪QQ7434510第四章数列夯实、拓展、感悟与提升第2页共16页学科网(北京)股份有限公司由,故选B(3)已知数列满足,(1)证明是等差数列,并求出公差;(2)求数列的通项公式.【解析】(1)由已知,,又,所以是以为首项,公差为的等差数列.(2)由(1)得当时,,验证与不符所以重点2等差数列及其性质、前项和例2(1)记为等差数列的前项和,若,则______.【解析】由已知,得【答案】100例2(2)在等差数列中,,则__________【解析】由等差数列的性质知.【答案】74贵州省凯里一中人教A版高中数学选择性必修第二册教学设计尹洪QQ7434510第四章数列夯实、拓展、感悟与提升第3页共16页学科网(北京)股份有限公司例2(3)已知为等差数列,其公差为,且是与的等比中项,为的前项和,则的值为()A.B.C.D.【解析】 ,∴,解之得,∴.故选D.例2(4)设等差数列的前项和为,若,,则当取最小值时等于()A.B.C.D.【解析】设该数列的公差为,则,解得,方法一:,所以当时,最小,故选A方法二:,由,因为,所以,于是当时,最小,故选A.例2(5)已知正项数列满足.(Ⅰ)求的值;(Ⅱ)求数列的通项公式;(Ⅲ)设数列的前项和为,不等式对任意的正整数恒成立,求实数的取值范围.【解析】(Ⅰ)当时,有,因为,所以.当时,有,解得.(Ⅱ)由于,①则有②②-①,得贵州省凯里一中人教A版高中数学选择性必修第二册教学设计尹洪QQ7434510第四章数列夯实、拓展、感悟与提升第4页共16页学科网(北京)股份有限公司由于0na,所以③同样有,,④③-④,得.所以,又,即对都成立所以数列是首项为1,公差为1的等差数列.所以nan.(Ⅲ)所以又所以数列是递增数列,故要使不等式对任意的正整数恒成立只须,又,所以所以实数a的取值范围是重点3等比数列及其性质、前项和例3(1)若等比数列满足,则公比为()A.B.C.D.贵州省凯里一中人教A版高中数学选择性必修第二册教学设计尹洪QQ74345...