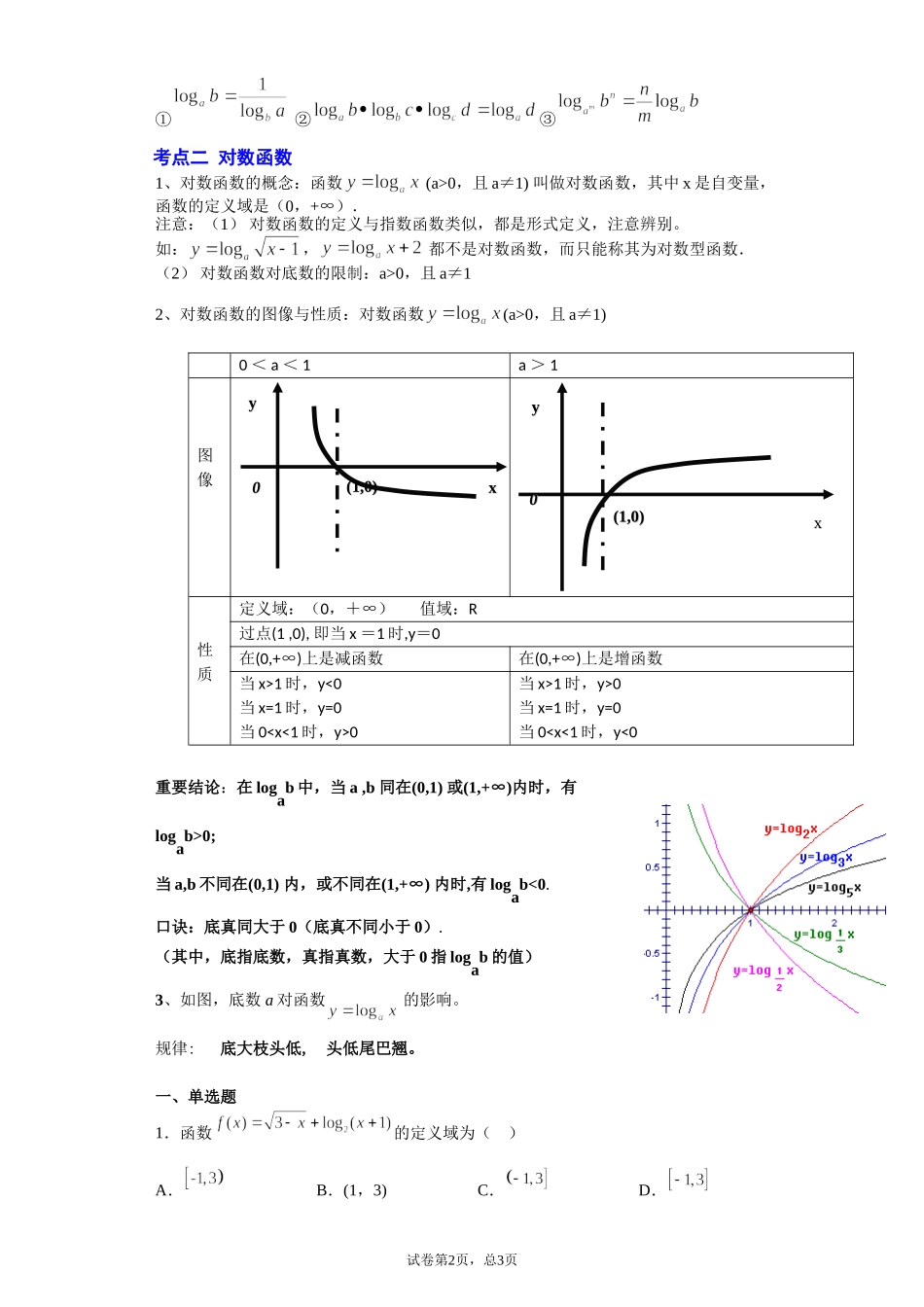
第四章对数运算与对数函数知识点与基础检测题考点一对数运算1.对数的概念:一般地,如果,那么数x叫做以a为底N的对数,记作:(a—底数,N—真数,—对数式)说明:1.注意底数的限制,a>0且a≠1;2.真数N>03.注意对数的书写格式.2、两个重要对数:(1)常用对数:以10为底的对数,;(2)自然对数:以无理数e为底的对数的对数,.3、对数式与指数式的互化对数式指数式对数底数←a→幂底数对数←x→指数真数←N→幂结论:(1)负数和零没有对数(2)logaa=1,loga1=0特别地,lg10=1,lg1=0,lne=1,ln1=0(3)对数恒等式:对数的运算性质如果a>0,a1,M>0,N>0有:1、两个正数的积的对数等于这两个正数的对数和2、两个正数的商的对数等于这两个正数的对数差3、一个正数的n次方的对数等于这个正数的对数n倍说明:1)简易语言表达:”积的对数=对数的和”……2)有时可逆向运用公式3)真数的取值必须是(0,+∞)4)特别注意:注意:换底公式利用换底公式推导下面的结论试卷第1页,总1页①②③考点二对数函数1、对数函数的概念:函数(a>0,且a≠1)叫做对数函数,其中x是自变量,函数的定义域是(0,+∞).注意:(1)对数函数的定义与指数函数类似,都是形式定义,注意辨别。如:,都不是对数函数,而只能称其为对数型函数.(2)对数函数对底数的限制:a>0,且a≠12、对数函数的图像与性质:对数函数(a>0,且a≠1)0<a<1a>1图像性质定义域:(0,+∞)值域:R过点(1,0),即当x=1时,y=0在(0,+∞)上是减函数在(0,+∞)上是增函数当x>1时,y<0当x=1时,y=0当00当x>1时,y>0当x=1时,y=0当00;当a,b不同在(0,1)内,或不同在(1,+∞)内时,有logab<0.口诀:底真同大于0(底真不同小于0).(其中,底指底数,真指真数,大于0指logab的值)3、如图,底数a对函数的影响。规律:底大枝头低,头低尾巴翘。一、单选题1.函数的定义域为()A.B.(1,3)C.D.试卷第2页,总3页yyxx00(1,0)(1,0)yyxx00(1,0)(1,0)2.已知,则的值为()A.3B.6C.9D.3.已知,,,则()A.a>c>bB.a>b>cC.c>a>bD.c>b>a4.()A.B.C.D.5.若函数,则的值()A.3B.2C.D.6.牛顿曾经提出了常温环境下的温度冷却模型:(为时间,单位分钟,为环境温度,为物体初始温度,为冷却后温度),假设一杯开水温度℃,环境温度℃,常数,大约经过多少分钟水温降为40℃?(结果保留整数,参考数据:)()A.9B...