第十一章 立体几何大题综合 讲义-2021-2022学年高中数学人教B版（2019）必修第四册.docxVIP免费

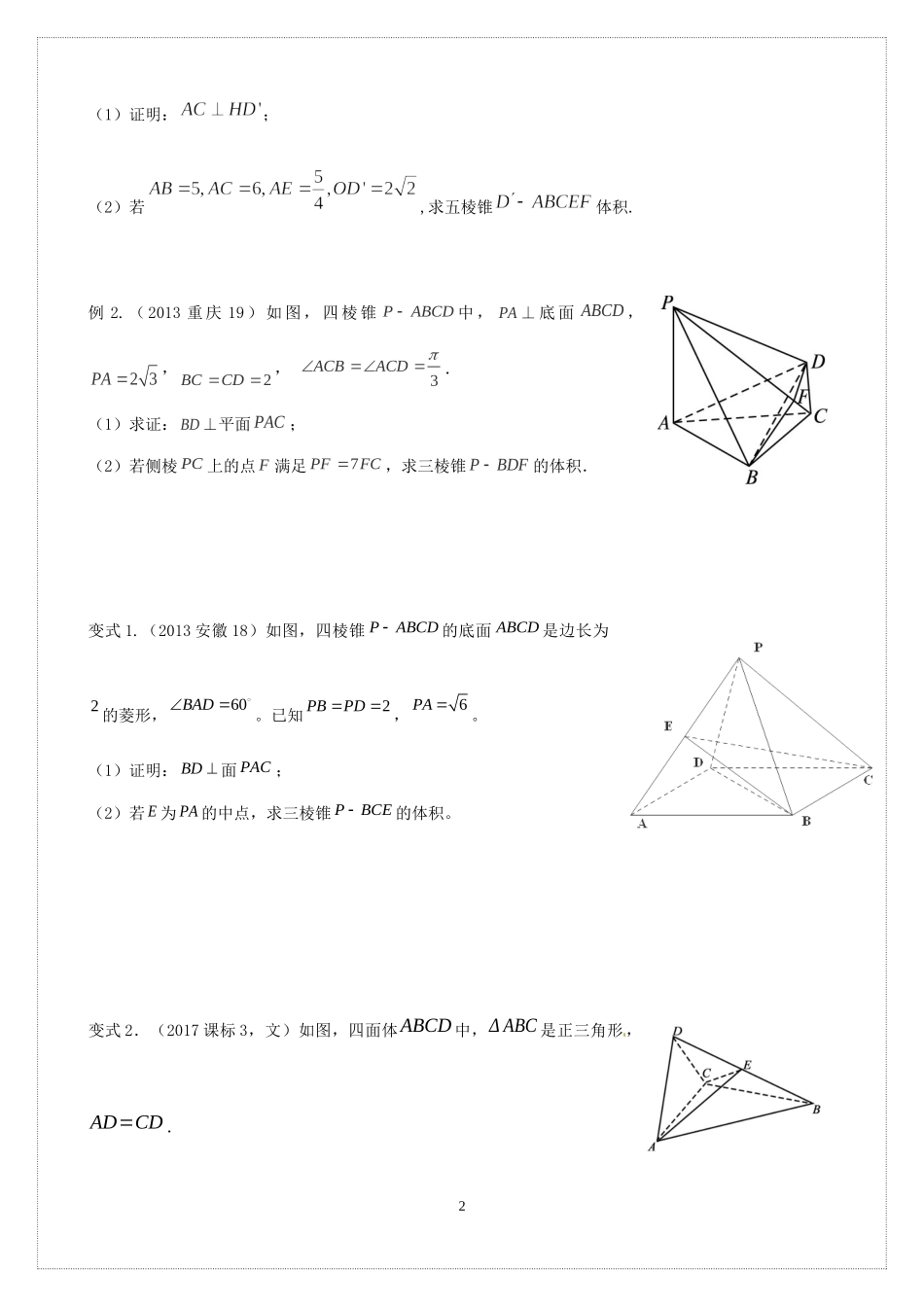
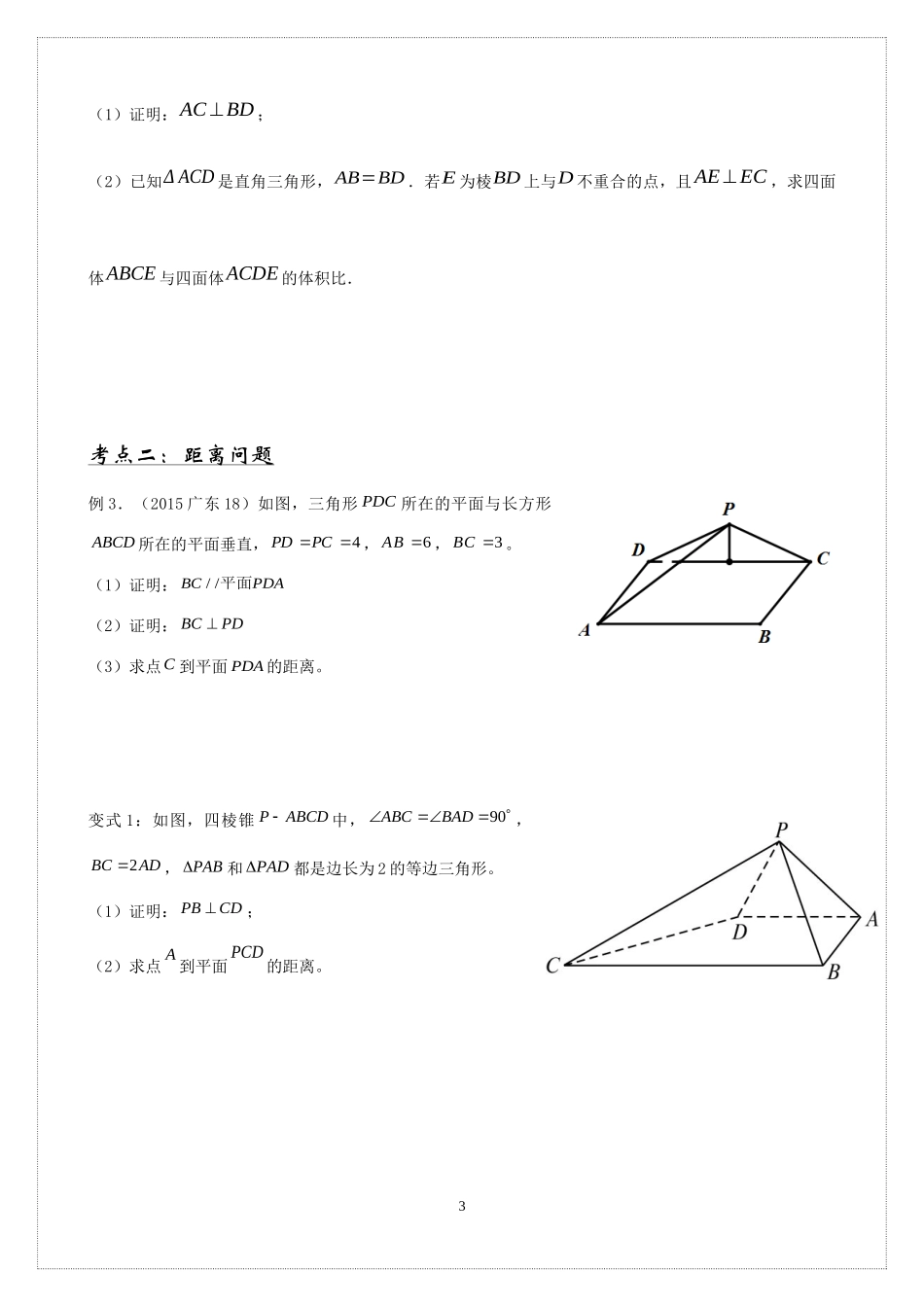
111.5立体几何大题综合（补充）（新课）典例解析考点一：体积问题例1．（2017课标II，文）如图，四棱锥中，侧面为等边三角形且垂直于底面,（1）证明：直线平面;（2）若△面积为，求四棱锥的体积.变式1.（2014辽宁19）如图，ABC和BCD所在平面互相垂直，且2ABBCBD，120ABCDBC，,,EFG分别为,,ACDCAD的中点.（1）求证：EF平面BCG；（2）求三棱锥DBCG的体积.变式2.（2016年高考新课标Ⅱ卷文）如图，菱形的对角线与交于点，点、分别在，上，，交于点，将沿折到的位置.GFEBCDA2（1）证明：；（2）若,求五棱锥体积.例2.（2013重庆19）如图，四棱锥PABCD中，PA⊥底面ABCD，23PA，2BCCD，3ACBACD．（1）求证：BD⊥平面PAC；（2）若侧棱PC上的点F满足7PFFC，求三棱锥PBDF的体积．变式1.（2013安徽18）如图，四棱锥PABCD的底面ABCD是边长为2的菱形，60BAD。已知2PBPD，6PA。（1）证明：BD面PAC；（2）若E为PA的中点，求三棱锥PBCE的体积。变式2．（2017课标3，文）如图，四面体ABCD中，ΔABC是正三角形，AD=CD．3（1）证明：AC⊥BD；（2）已知ΔACD是直角三角形，AB=BD．若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．考点二：距离问题例3．（2015广东18）如图，三角形所在的平面与长方形所在的平面垂直，，，。（1）证明：（2）证明：（3）求点到平面的距离。变式1：如图，四棱锥中，，，和都是边长为2的等边三角形。（1）证明：；（2）求点到平面的距离。PDCABCD4PDPC6AB3BC//BCPDA平面BCPDCPDAPABCD90ABCBAD2BCADPABPADPBCDAPCD4变式2．如图，在四棱锥中，，，，．（1）求证：；（2）求点到平面的距离．考点三：夹角问题例4．如图，已知四棱锥的底面是边长为2的菱形，，，，点E，F分别是，的中点．（1）求证：平面；（2）求异面直线与所成角的正弦值；变式1．如图，正三棱柱为棱的中点.（1）证明：平面；（2）证明：平面平面；（3）求直线与平面所成角的正弦值.5变式2．如图，四棱锥中，平面，，，，为线段上一点，且．（1）证明：平面平面；（2）求二面角的余弦值．巩固练习1.（2017北京，文）如图，在三棱锥P−ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D为线段AC的中点，E为线段PC上一点．（1）求证：PA⊥BD；（2）求证：平面BDE⊥¿¿平面PAC；（3）当平面BDE时，求三棱锥E−BCD的体积．2.（2015北京文18）如图所示，在三...