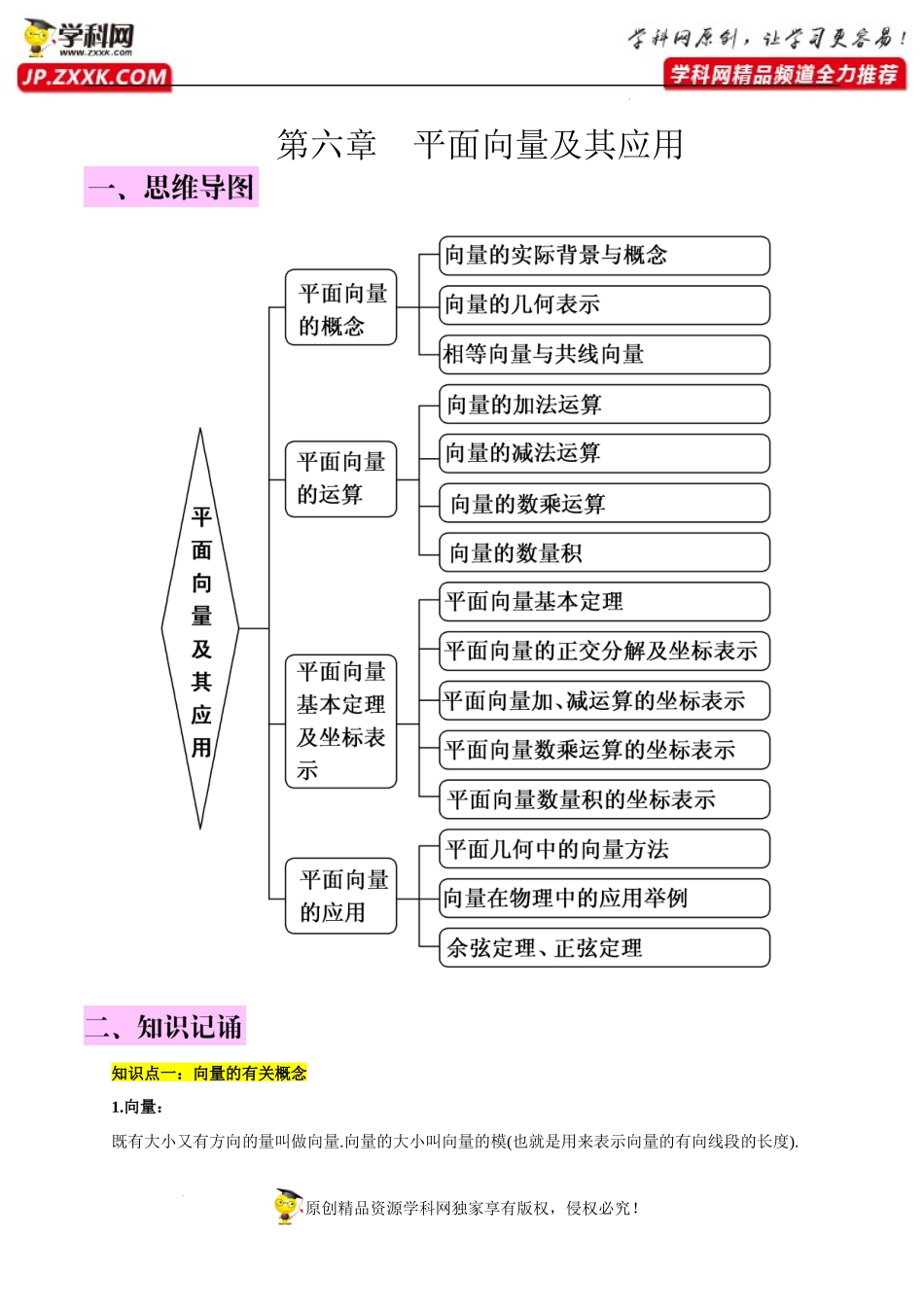
原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司第六章平面向量及其应用知识点一:向量的有关概念1.向量:既有大小又有方向的量叫做向量.向量的大小叫向量的模(也就是用来表示向量的有向线段的长度).原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司2.向量的表示方法:(1)字母表示法:如等.(2)几何表示法:用一条有向线段表示向量.如,等.(3)坐标表示法:在平面直角坐标系中,设向量的起点为在坐标原点,终点A坐标为,则称为的坐标,记为=.3.相等向量:长度相等且方向相同的向量.向量可以自由平移,平移前后的向量相等.两向量与相等,记为.4.零向量:长度为零的向量叫零向量.零向量只有一个,其方向是任意的.5.单位向量:长度等于1个单位的向量.单位向量有无数个,每一个方向都有一个单位向量.6.共线向量:方向相同或相反的非零向量,叫共线向量.任一组共线向量都可以移到同一直线上.规定:与任一向量共线.注:共线向量又称为平行向量.7.相反向量:长度相等且方向相反的向量.知识点二、向量的运算1.运算定义运算图形语言符号语言坐标语言加法与减法+==记=(x1,y1),=(x2,y2)则=(x1+x2,y1+y2)=(x2-x1,y2-y1)原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司+=实数与向量的乘积记=(x,y)则两个向量的数量积记则=x1x2+y1y22.运算律加法:①(交换律);②(结合律)实数与向量的乘积:①;②;③两个向量的数量积:①·=·;②()·=·()=(·);③(+)·=·+·3.运算性质及重要结论(1)平面向量基本定理:如果是同一平面内两个不共线的向量,那么对于这个平面内任一向量,有且只有一对实数,使,称为的线性组合.①其中叫做表示这一平面内所有向量的基底;②平面内任一向量都可以沿两个不共线向量的方向分解为两个向量的和,并且这种分解是唯一的.③当基底是两个互相垂直的单位向量时,就建立了平面直角坐标系,因此平面向量基本定理实际上是平面向量坐标表示的基础.向量坐标与点坐标的关系:当向量起点在原点时,定义向量坐标为终点坐标,原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司即若A(x,y),则OA−−→=(x,y);当向量起点不在原点时,向量AB−−→坐标为终点坐标减去起点坐标,即若A(x1,y1),B(x2,y2),则AB−−→=(x2-x1,y2-y1)(2)两个向量平行的充要条件符号语言:a→//b→⇔a→=λb→(b→≠0→)坐标语言为:设非零向量,则∥⇔(x1,y1)=(x2,...