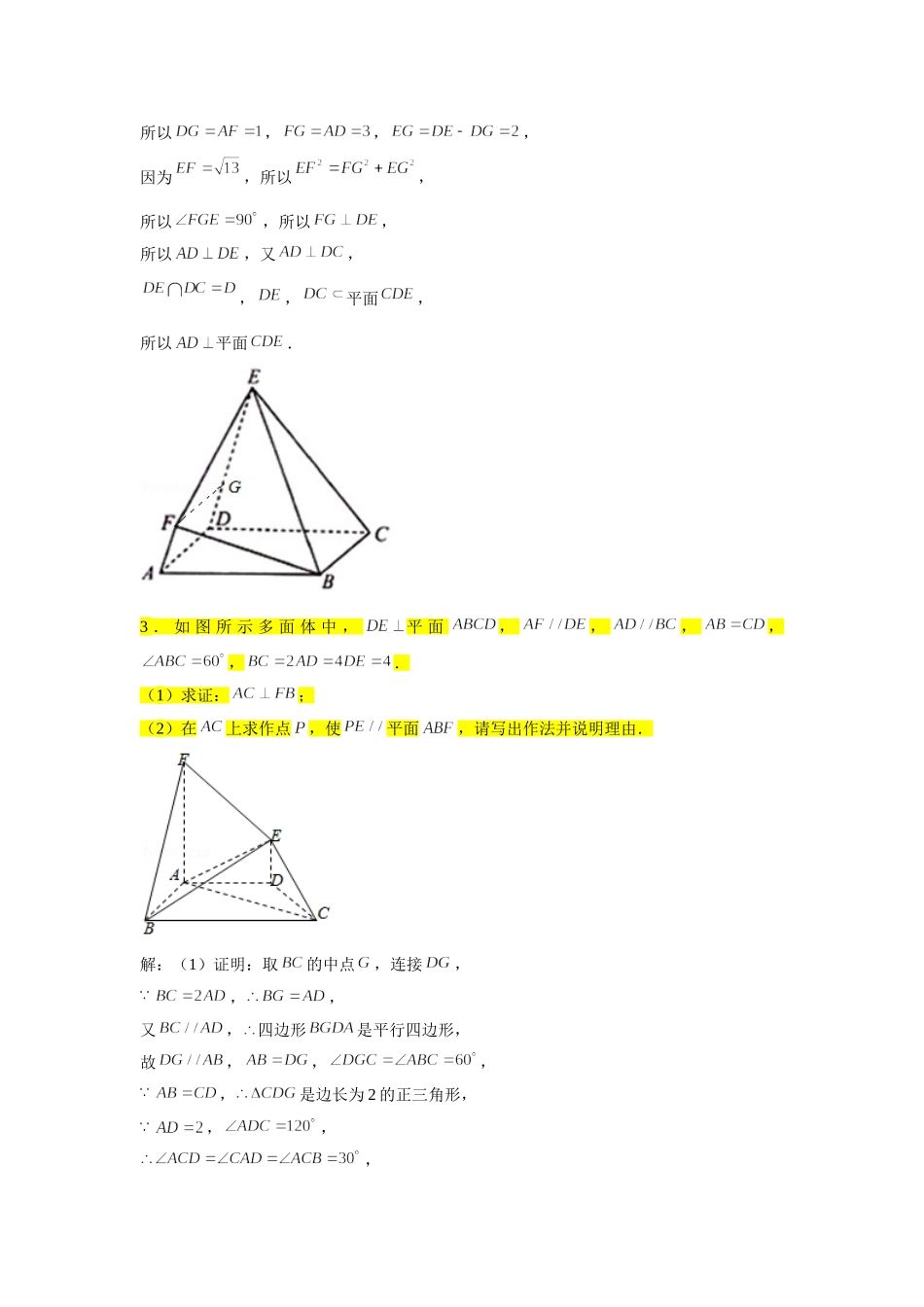
第八章立体几何专题训练(十一)—证明平行、垂直(2)1.如图,在三棱柱中,平面平面,,,,,为的中点.(1)求证:平面;(2)求证:平面.证明:(1)取中点,连接,,在三棱柱中,为的中点.,,四边形是平行四边形,,,平面,平面,,平面,平面,平面平面,平面,平面.(2),为的中点,,又平面平面,平面平面,平面,平面,又平面,.又,,面.2.在如图所示的多面体中,是正方形,,,,四点共面,面.(1)求证:面;(2)若,,,求证:平面.证明:(1)因为是正方形,所以,又面,面,所以面,因为面,,,平面,所以面面,又面,所以面.(2)在平面中,作交于点,因为面,平面,平面平面,所以,又,所以四边形为平行四边形,所以,,,因为,所以,所以,所以,所以,又,,,平面,所以平面.3.如图所示多面体中,平面,,,,,.(1)求证:;(2)在上求作点,使平面,请写出作法并说明理由.解:(1)证明:取的中点,连接,,,又,四边形是平行四边形,故,,,,是边长为2的正三角形,,,,,即,平面,,平面,,,又,所以,,又,,平面,平面,又平面,,平面,平面,,平面,平面,.(2)设交于点,连接,此时点即为所求作的点.证明如下:,,又,四边形是平行四边形,故,即,又平面,平面,平面.,平面,平面,平面.又平面,平面,,平面平面,平面,平面.4.如图,在四棱锥中,平面,,,,.(1)求证:平面平面;(2)若点满足,且平面,求的值.解:(1)证明:由平面,可得,又,,可得,由平面,,可得平面,,又,,可得,在中,,,,可得,即为,解得,由,可得,又,而,为平面内的两条相交直线,所以平面,又平面,所以平面平面;(2)连接与交于,连接,由平面,平面,平面平面,可得,所以,在四边形中,,可得,所以.5.如图1,C,D是以AB为直径的圆上两点,且2ABAD,ACBC,将ABC所在的半圆沿直径AB折起,使得点C在平面ABD上的正投影E在线段BD上,如图2.(1)求证:BC平面ACD;(2)已知O为AB中点,在线段CE上是否存在点F,使得//OF平面ACD?若存在,求出CFFE的值;若不存在,请说明理由.(1)证明:由图1可知:ADBD,ACBC,由图2,E为C在平面BAD的投影,CE平面ABD,AD面ABD,CEAD,BDCDD,AD面BCD,BC面BCD,ADBC,ADACA,BC面ACD.(2)解:不存在.不妨令2AB,则1AD,3BD,2ACBC,22CO.ABCD,ABCE,CDCEC,...