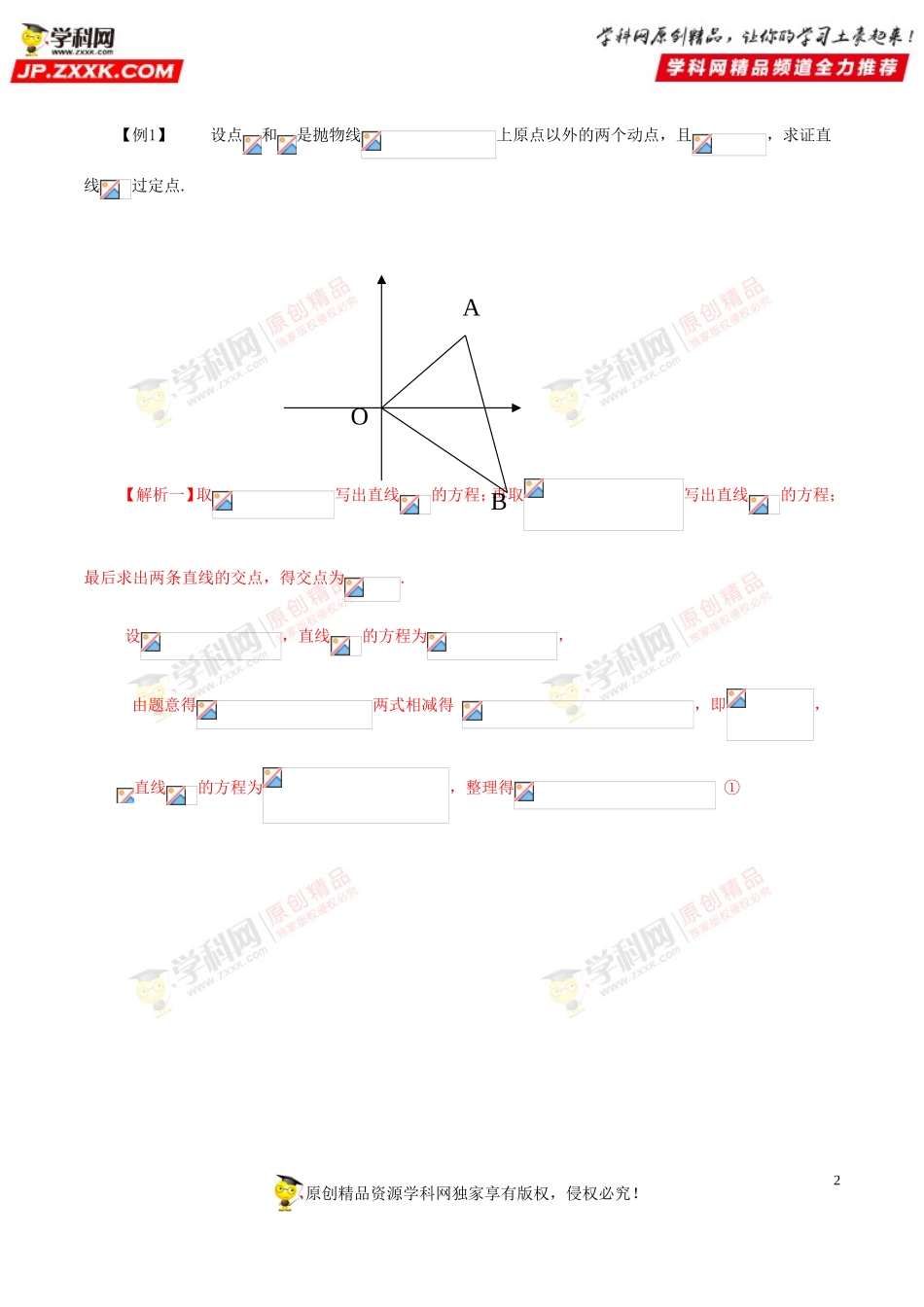
1【知识要点】一、定点问题:对满足一定条件曲线上两点连结所得直线过定点或满足一定条件的曲线过定点问题,证明直线过定点,一般有两种方法.(1)特殊探求,一般证明:即可以先考虑动直线或曲线的特殊情况,找出定点的位置,然后证明该定点在该直线或该曲线上(定点的坐标直线或曲线的方程后等式恒成立).(2)分离参数法:一般可以根据需要选定参数,结合已知条件求出直线或曲线的方程,分离参数得到等式,(一般地,为关于的二元一次关系式)由上述原理可得方程组,从而求得该定点.二、定值问题:在几何问题中,有些几何量与参数无关,这就构成了定值问题,定值问题的处理常见的方法有:(1)特殊探究,一般证明.(2)直接求题目给定的对象的值,证明其结果是一个常数.【方法讲评】题型一定点问题方法一特殊探求,一般证明:即可以先考虑动直线或曲线的特殊情况,找出定点的位置,然后证明该定点在该直线或该曲线上(定点的坐标直线或曲线的方程后等式恒成立).方法二分离参数法:若等式对恒成立,则同时成立,运用这一原理,可以证明直线或曲线过定点问题.一般可以根据需要选定参数,结合已知条件求出直线或曲线的方程,分离参数得到等式,(一般地,为关于的二元一次关系式)由上述原理可得方程组,从而求得该定点.原创精品资源学科网独家享有版权,侵权必究!2【例1】设点和是抛物线上原点以外的两个动点,且,求证直线过定点.【解析一】取写出直线的方程;再取写出直线的方程;最后求出两条直线的交点,得交点为.设,直线的方程为,由题意得两式相减得,即,直线的方程为,整理得①原创精品资源学科网独家享有版权,侵权必究!OAB3【点评】(1)证明直线过定点,一般有两种方法.方法一:特殊探求,一般证明:即可以先考虑动直线或曲线的特殊情况,找出定点的位置,然后证明该定点在该直线或该曲线上(定点的坐标直线或曲线的方程后等式恒成立).方法二:分离参数法:若等式对恒成立,则同时成立,运用这一原理,可以证明直线或曲线过定点问题.一般可以根据需要选定参数,结合已知条件求出直线或曲线的方程,分离参数得到等式,(一般地,为关于的二元一次关系式)由上述原理可得方程组,从而求得该定点.(2)解析一使用的就是方法一,解析二使用的就是方法二.大家注意灵活选择.学科#网【反馈检测1】已知椭圆的中心在坐标原点,焦点在轴上,椭圆上的点到焦点距离的最大值为,最小值为.(Ⅰ)求椭圆的标准方程;(Ⅱ)若直线与椭圆相交于,两...