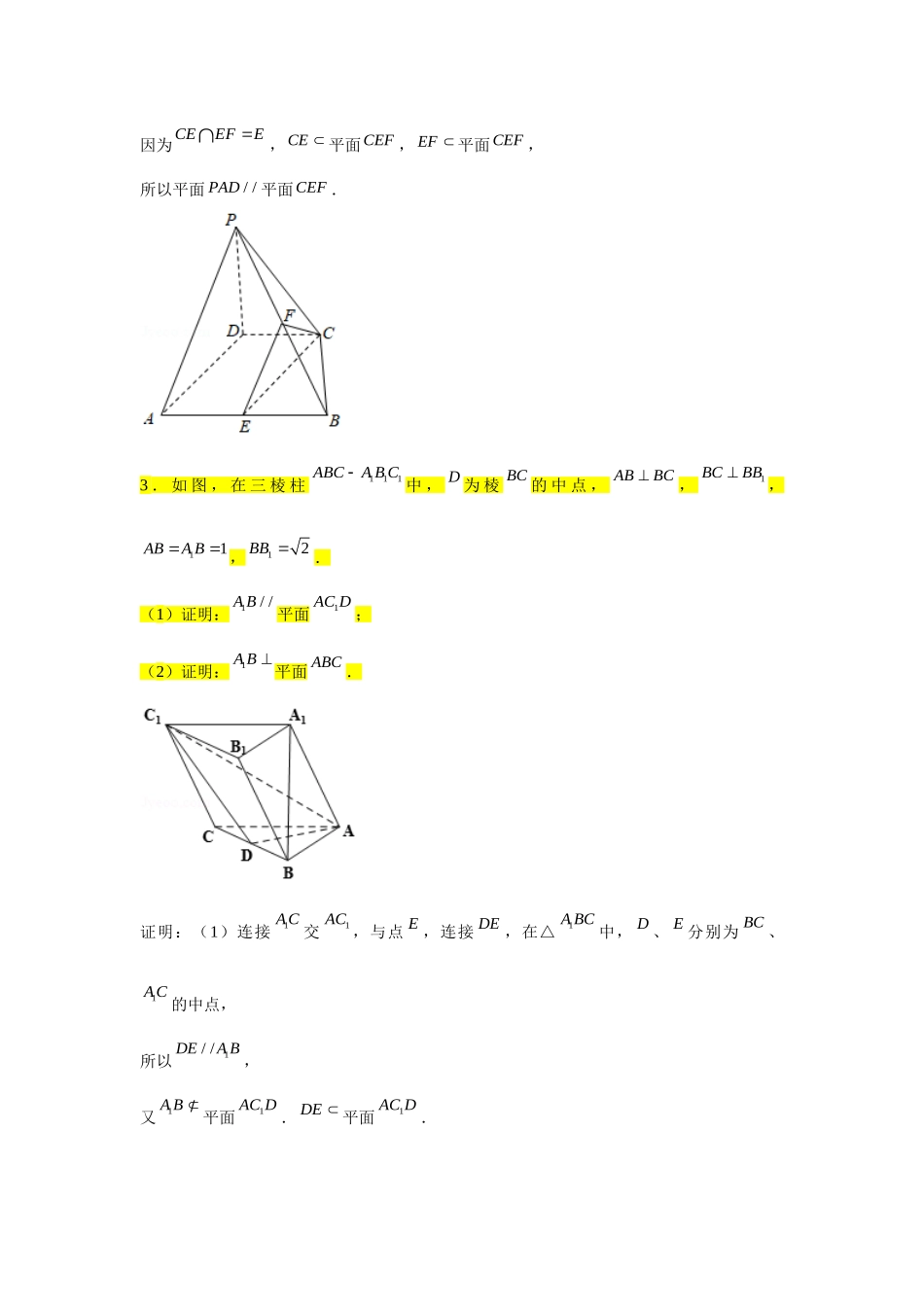
第八章立体几何专题训练(十)—证明平行、垂直(1)1.如图.在直四棱柱中,E,F分别AB,BC的中点,11AC与11BD交于点O.(1)求证:1A,1C,F,E四点共面;(2)若底面ABCD是菱形,且1ODAE,求证:OD平面11ACFE.解:(1)连接AC,因为E,F分别是AB,BC的中点,所以EF是ABC的中位线,所以//EFAC,由直棱柱知://11AACC,所以四边形11AACC为平行四边形,所以11//ACAC,5分所以11//EFAC,故1A,1C,F,E四点共面;7分,(2)连接BD,因为直棱柱中1DD平面1111ABCD,11AC平面1111ABCD,所以111DDAC,因为底面1111ABCD是菱形,所以1111ACBD,又1111DDBDD,所以11AC平面11BBDD,11分因为OD平面11BBDD,所以11ODAC,又1ODAE,1111ACAEA,11AC平面11ACFE,1AE平面11ACFE,所以OD平面1114ACFE分2.如图,在四棱锥PABCD中,223ABCD,2PD,7PC,//CDAB,PDBC,E,F分别为棱AB,PB的中点.(1)证明:PD平面ABCD.(2)证明:平面//PAD平面CEF.证明:(1)因为3CD,2PD,7PC,所以222CDPDPC,所以PDDC.因为PDBC,DCBCC,所以PD平面ABCD.(2)因为E为棱AB的中点,所以12AEAB.因为2ABCD,所以AECD,因为//CDAB,所以//AECD,所以四边形AECD为平行四边形,所以//CEAD,所以//CE平面PAD.因为E,F分别为棱AB,PB的中点,所以//EFPA,所以//EF平面PAD.因为CEEFE,CE平面CEF,EF平面CEF,所以平面//PAD平面CEF.3.如图,在三棱柱111ABCABC中,D为棱BC的中点,ABBC,1BCBB,11ABAB,12BB.(1)证明:1//AB平面1ACD;(2)证明:1AB平面ABC.证明:(1)连接1AC交1AC,与点E,连接DE,在△1ABC中,D、E分别为BC、1AC的中点,所以1//DEAB,又1AB平面1ACD.DE平面1ACD.所以1//AB平面1ACD.(2)因为ABBC,1BCBB,1ABBBB,AB、1BB平面1ABB.所以BC平面1ABB,又1AB平面1ABB.所以1ABBC;又因为1111,2ABABBBAA,得22211AAABAB,所以1ABAB.又AB,BC平面ABCABBCB,所以1AB平面ABC.4.如图,四面体ABCD中,BCCD,90BCD,AD平面BCD.M为AD中点,P为BM中点,点Q在线段AC上,且3AQQC.(1)求证://PQ平面BCD;(2)若ADDC,N是CD的中点,求证:NQ平面ABC.证明:(1)如图,取BD的中点为E,在CD上取一点F,使得3DFFC,连结EP,FQ,EF,则由P,E分别为BM,DB的中点,可得//PEDM,且12PED...