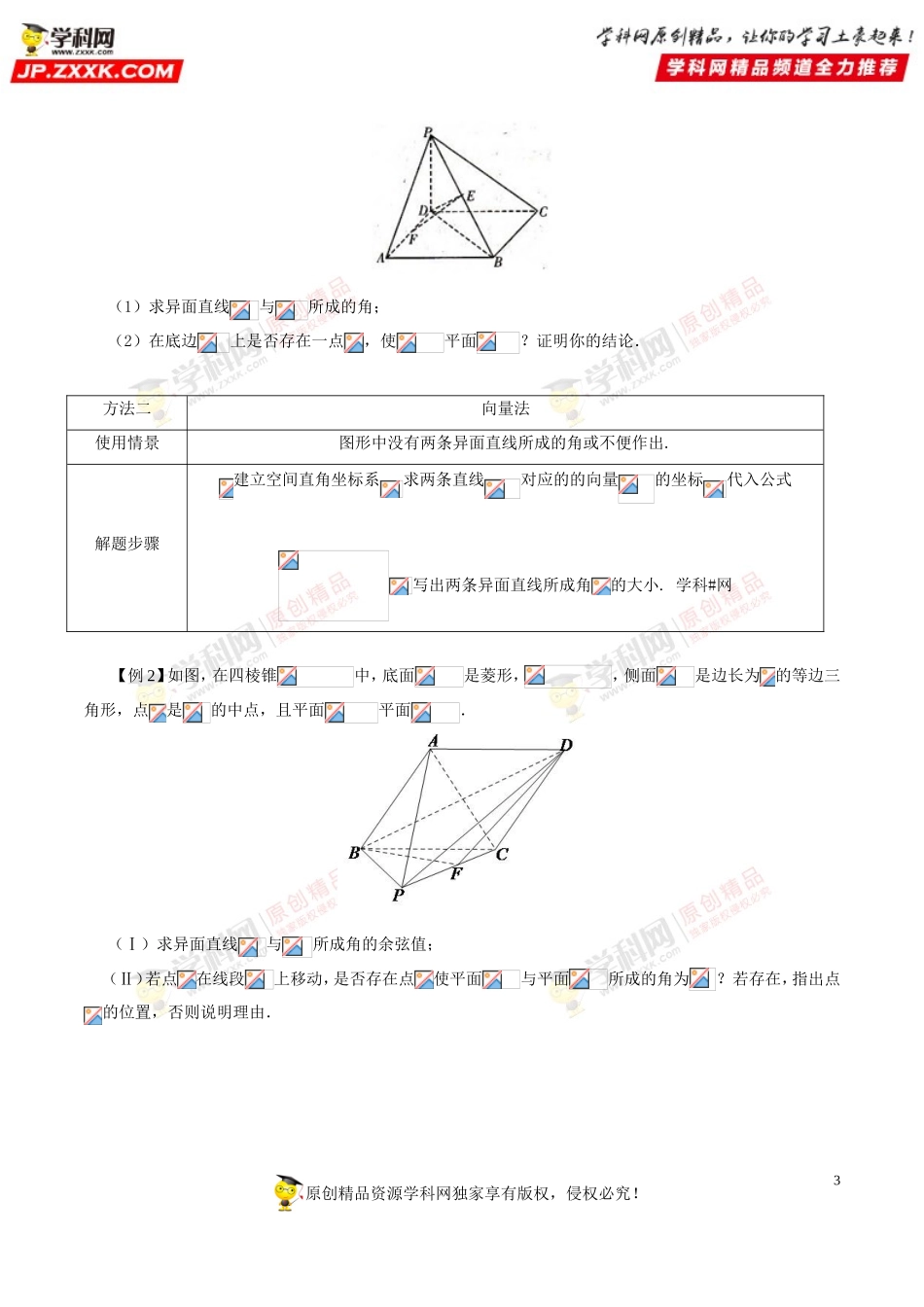
1【知识要点】一、异面直线的定义:直线是异面直线,经过空间任意一点,分别引直线∥,∥,我们把直线和所成的锐角(或直角)叫做异面直线和所成的角.二、异面直线所成的角的范围:三、异面直线所成的角的求法方法一:(几何法)找作(平移法、补形法)证(定义)指求(解三角形)方法二:(向量法),其中是异面直线所成的角,分别是直线的方向向量.四、求异面直线所成的角体现的是数学的转化的思想,就是把空间的角转化为平面的角,再利用解三角形的知识解答.五、温馨提示如果你解三角形得到的角的余弦是一个负值,如,你不能说两条异面直线所成的角为,你应该说两条异面直线所成的角为,因为两条异面直线所成的角的范围为.【方法讲评】方法一几何法使用情景图形中两条异面直线所成的角本身就存在或很方便就能作出.解题步骤找作(平移法、补形法)证(定义)指求(解三角形)【例1】如下左图,在中,,,是上的高,沿将原创精品资源学科网独家享有版权,侵权必究!2折成的二面角,如下右图.(1)证明:平面平面;(2)设为的中点,,求异面直线和所成的角的大小.【解析】(1)因为折起前是边上的高,则当折起后,,,又,则平面.因为平面,所以平面平面.【点评】(1)本题中异面直线与所成的角可以通过平移的方法作出,为异面直线与所成的角.再利用余弦定理解即得.(2)利用几何法求异面直线所成的角,经常要解直角三角形或斜三角形,所以要用到直角三角函数或正余弦定理.【反馈检测1】如图,四棱锥的底面是边长为2的正方形,底面,,为的中点.原创精品资源学科网独家享有版权,侵权必究!3(1)求异面直线与所成的角;(2)在底边上是否存在一点,使平面?证明你的结论.方法二向量法使用情景图形中没有两条异面直线所成的角或不便作出.解题步骤建立空间直角坐标系求两条直线对应的的向量的坐标代入公式写出两条异面直线所成角的大小.学科#网【例2】如图,在四棱锥中,底面是菱形,,侧面是边长为的等边三角形,点是的中点,且平面平面.(Ⅰ)求异面直线与所成角的余弦值;(Ⅱ)若点在线段上移动,是否存在点使平面与平面所成的角为?若存在,指出点的位置,否则说明理由.原创精品资源学科网独家享有版权,侵权必究!4(Ⅰ),,则,,设异面直线与所成角为,所以异面直线与所成角的余弦值为故,即,此时,点在延长线上,所以,在边上不存在点使平面与平面所成的角为原创精品资源学科网独家享有版权,侵权必究!5【点评】(1)异面直线与所成角...