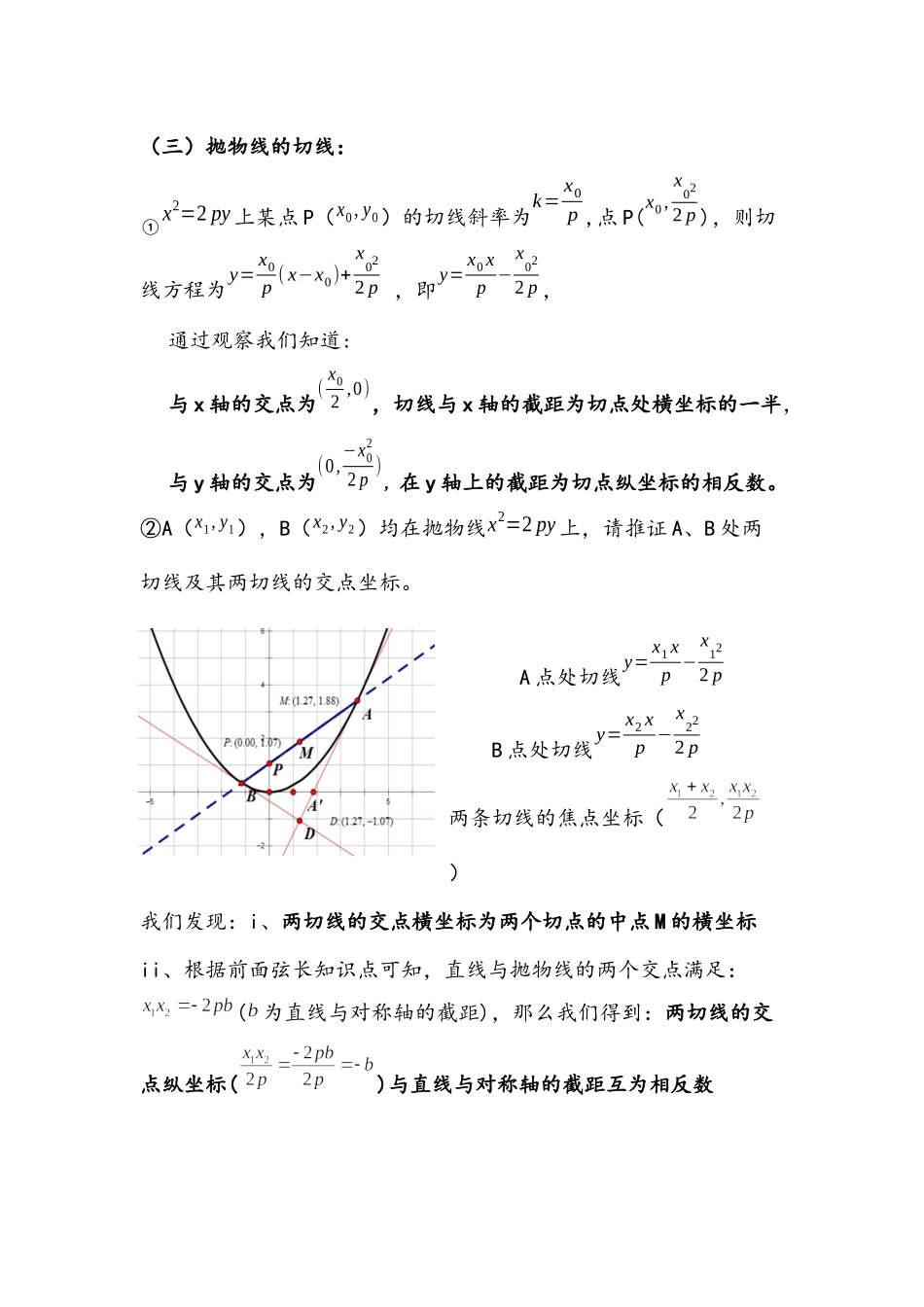
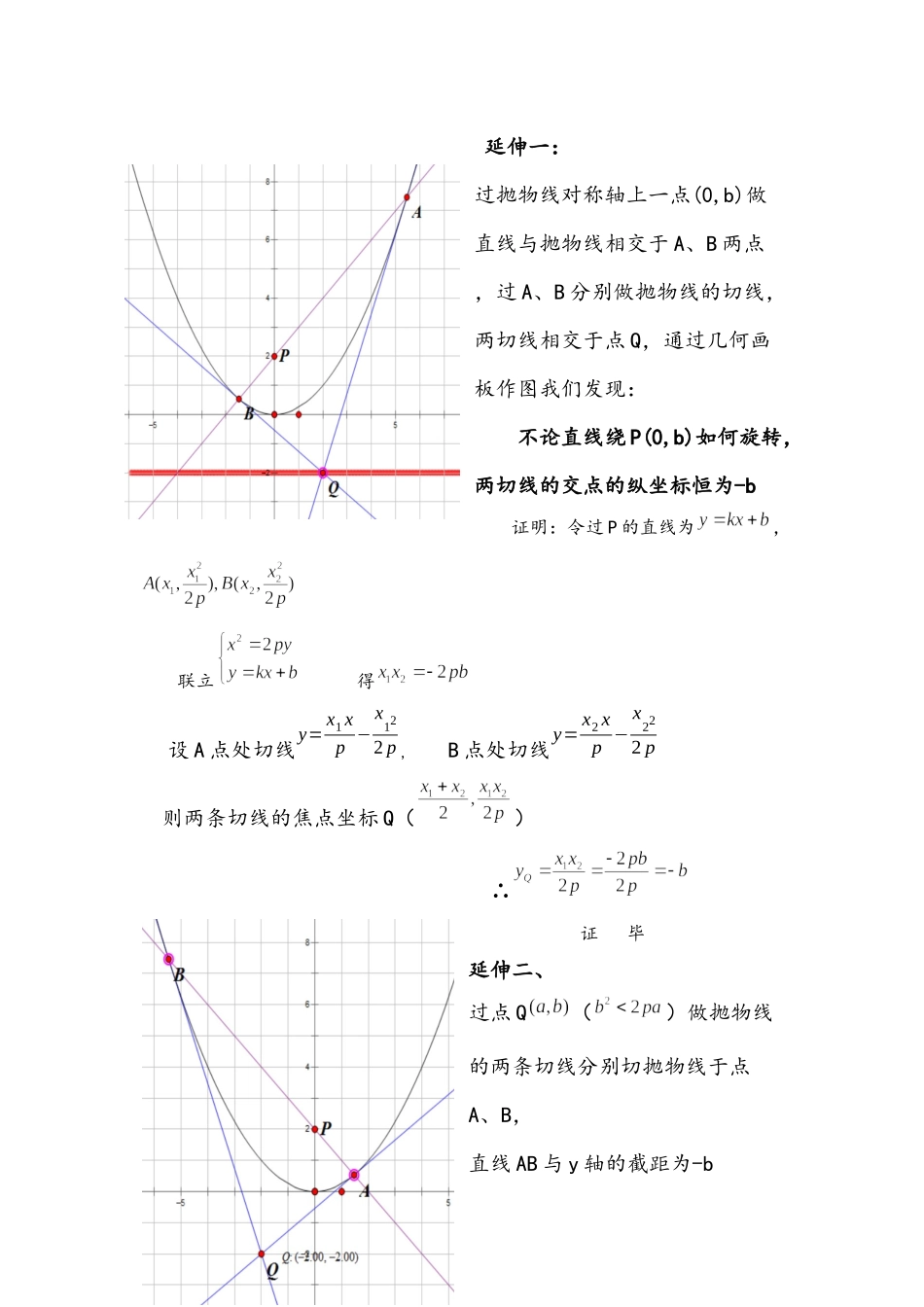
第12讲:圆锥曲线的切线不管是哪一种圆锥曲线的切线,其本质都是圆锥曲线与直线只有一个交点,即联立圆锥曲线方程与直线方程所得到的一元二次方程有且仅有一个根,即Δ=0,相信这对于大家来说都不是问题,在这里我们对圆锥曲线的切线做一些总结,以方便大家在最短的时间内解决题目。(一)椭圆的切线:①x2a2+y2b2=1在点P(x0,y0)处的切线方程为x0xa2+y0yb2=1②过椭圆外一点Q(x1,y1)可以做椭圆的两条切线,两切点所在的直线方程为x1xa2+y1yb2=1③直线y=kx+m与椭圆x2a2+y2b2=1相切时,满足a2k2+b2=m2例:已知P为椭圆x24+y23=1上一动点,求点P到直线2x−y−6=0的最小值与最大值。(二)双曲线的切线:①x2a2−y2b2=1在点P(x0,y0)处的切线方程为x0xa2−y0yb2=1②过椭圆外一点Q(x1,y1)可以做椭圆的两条切线,两切点所在的直线方程为x1xa2−y1yb2=1③直线y=kx+m与椭圆x2a2+y2b2=1相切时,满足a2k2−b2=m2(三)抛物线的切线:①x2=2py上某点P(x0,y0)的切线斜率为k=x0p,点P(x0,x022p),则切线方程为y=x0p(x−x0)+x022p,即y=x0xp−x022p,通过观察我们知道:与x轴的交点为(x02,0),切线与x轴的截距为切点处横坐标的一半,与y轴的交点为(0,−x022p),在y轴上的截距为切点纵坐标的相反数。②A(x1,y1),B(x2,y2)均在抛物线x2=2py上,请推证A、B处两切线及其两切线的交点坐标。A点处切线y=x1xp−x122pB点处切线y=x2xp−x222p两条切线的焦点坐标()我们发现:i、两切线的交点横坐标为两个切点的中点M的横坐标ii、根据前面弦长知识点可知,直线与抛物线的两个交点满足:(为直线与对称轴的截距),那么我们得到:两切线的交点纵坐标()与直线与对称轴的截距互为相反数延伸一:过抛物线对称轴上一点(0,b)做直线与抛物线相交于A、B两点,过A、B分别做抛物线的切线,两切线相交于点Q,通过几何画板作图我们发现:不论直线绕P(0,b)如何旋转,两切线的交点的纵坐标恒为-b证明:令过P的直线为,联立得设A点处切线y=x1xp−x122p,B点处切线y=x2xp−x222p则两条切线的焦点坐标Q()∴证毕延伸二、过点Q()做抛物线的两条切线分别切抛物线于点A、B,直线AB与y轴的截距为-b斜率∴切点弦方程为:③对于焦点在x轴上的抛物线,求切线一般联立方程,利用Δ=0求解。④需要需注意的是:过抛物线外一点做与抛物线仅有一个交点的直线有三条:除了两条切线之外还有一条与x轴平行(即斜率为0的直线与抛物线也只有一个交点。练习1.历史上第一个研究圆锥曲线的是梅纳库莫斯(公...