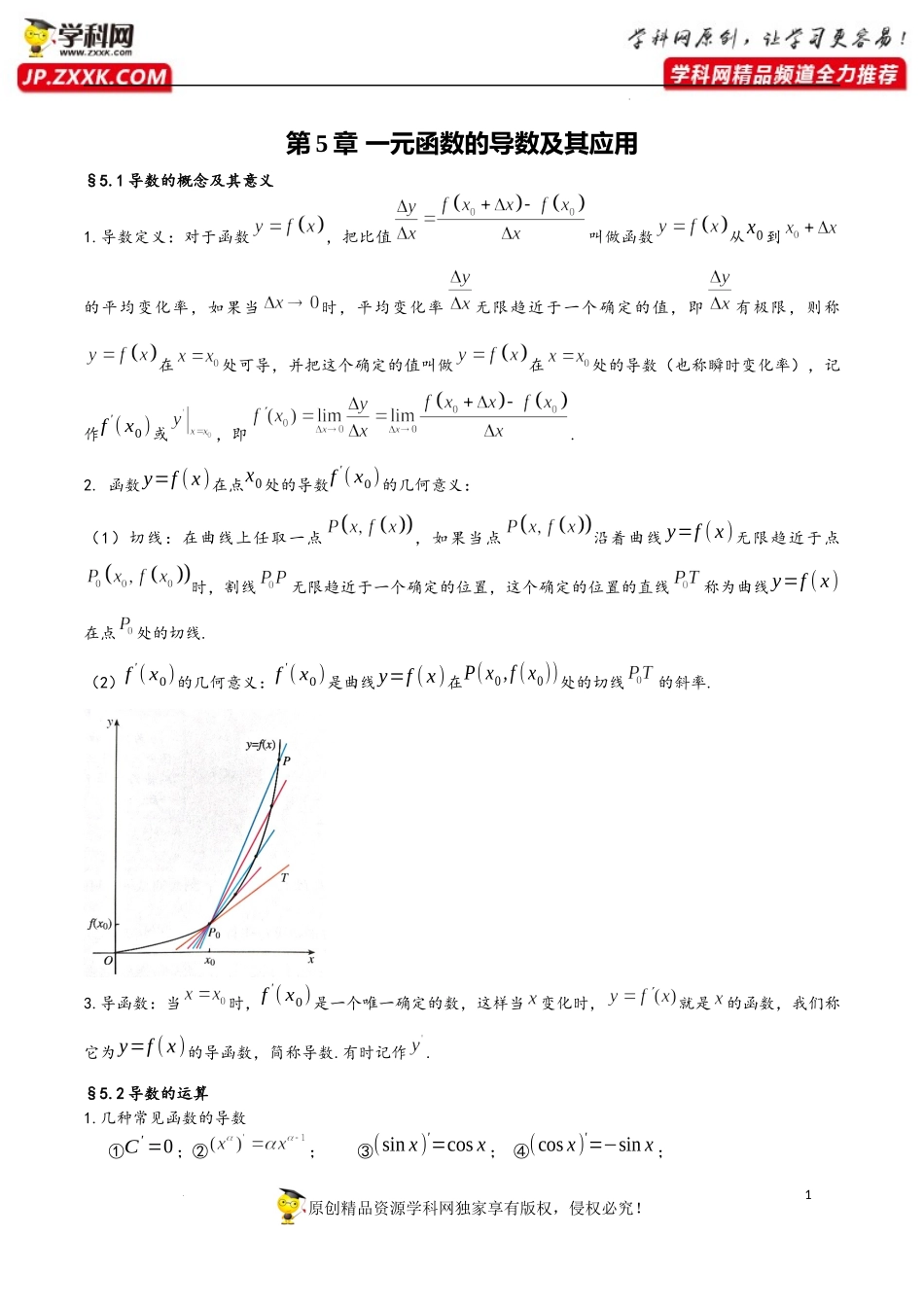
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司第5章一元函数的导数及其应用§5.1导数的概念及其意义1.导数定义:对于函数,把比值叫做函数从x0到的平均变化率,如果当时,平均变化率无限趋近于一个确定的值,即有极限,则称在处可导,并把这个确定的值叫做在处的导数(也称瞬时变化率),记作f'(x0)或,即.2.函数y=f(x)在点x0处的导数f'(x0)的几何意义:(1)切线:在曲线上任取一点,如果当点沿着曲线y=f(x)无限趋近于点时,割线无限趋近于一个确定的位置,这个确定的位置的直线称为曲线y=f(x)在点处的切线.(2)f'(x0)的几何意义:f'(x0)是曲线y=f(x)在P(x0,f(x0))处的切线的斜率.3.导函数:当时,f'(x0)是一个唯一确定的数,这样当变化时,就是的函数,我们称它为y=f(x)的导函数,简称导数.有时记作.§5.2导数的运算1.几种常见函数的导数①C'=0;②;③(sinx)'=cosx;④(cosx)'=−sinx;2原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司⑤(ax)'=axlna;⑥(ex)'=ex;⑦(logax)'=1xlna;⑧(lnx)'=1x2.导数的四则运算法则(1).(2).特别地:.(3).3.复合函数求导法则由函数复合而成的的函数的导数和函数的导数间的关系为,即对的导数等于对的导数与对的导数的乘积.§5.3导数在研究函数中的应用1.导数与函数的单调性(1)在某个区间上,如果f'(x)>0,则函数在区间上为单调递增;在某个区间上,如果,则函数在区间上为单调递减.(2)设函数y=f(x)在某个区间内可导,若f(x)为增函数,则(在上的任何子区间内都不恒等于零);若f(x)为减函数,则(在上的任何子区间内都不恒等于零).2.函数的极值函数在点的函数值比它在点附近其他点的函数值都小,,而且在点附近的左侧,右侧f'(x)>0,我们把叫做函数的极小值点,叫做函数的极小值;函数在点的函数值比它在点附近其他点的函数值都大,,而且在点附近的左侧,右侧,我们把叫做函数的极大值点,叫做函数的极大值.极小值点和极大值点统称为极值点,极小值和极大值统称为极值.3.最大值、最小值:设函数的定义域为,3原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司如果存在实数满足:(1),都有;(2)使得,我们就称是函数的最大值.如果存在实数满足:(1),都有;(2)使得,我们就称是函数的最小值.4原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司