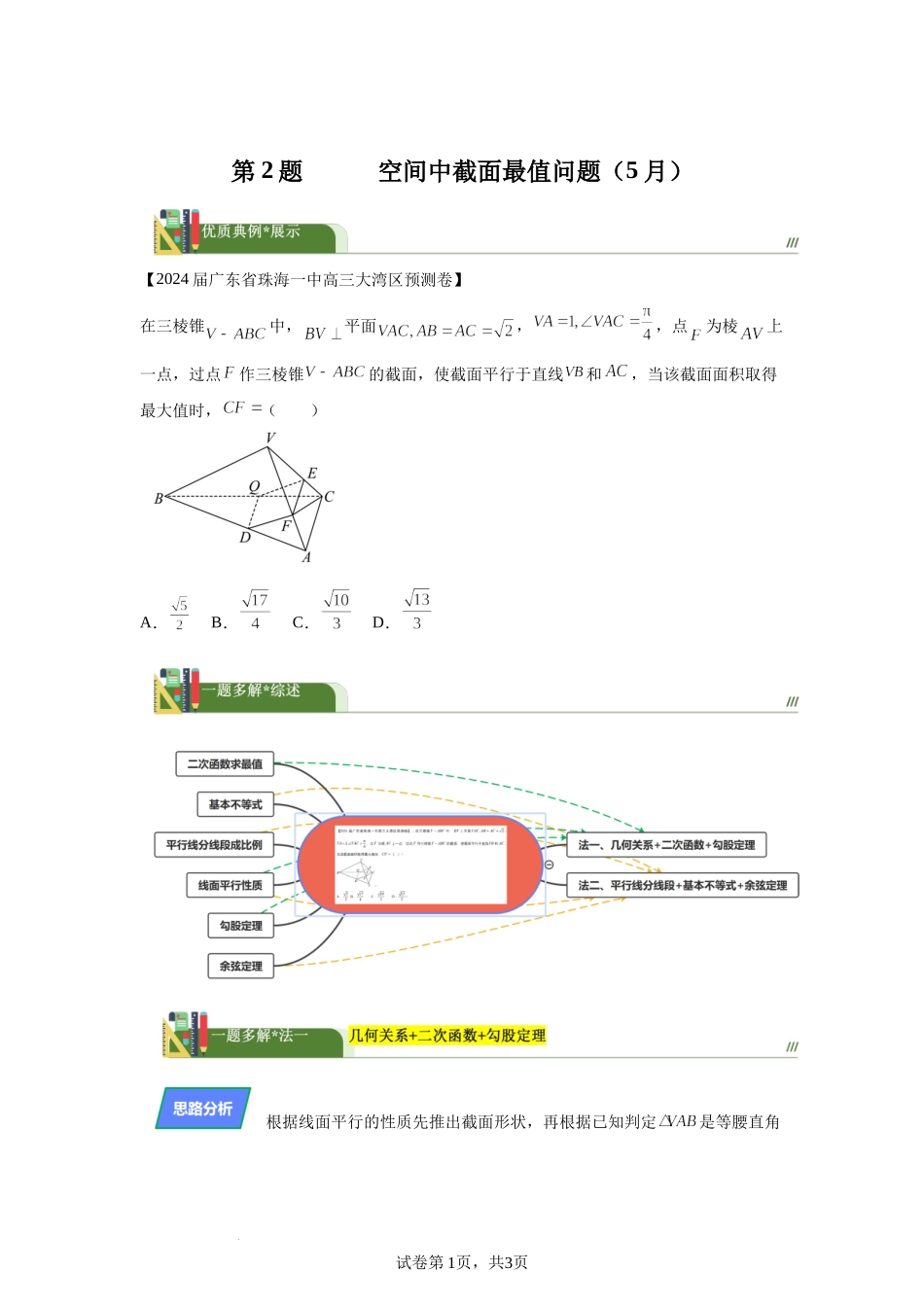
试卷第1页,共3页学科网(北京)股份有限公司第2题空间中截面最值问题(5月)【2024届广东省珠海一中高三大湾区预测卷】在三棱锥中,平面,,点为棱上一点,过点作三棱锥的截面,使截面平行于直线和,当该截面面积取得最大值时,()A.B.C.D.根据线面平行的性质先推出截面形状,再根据已知判定是等腰直角试卷第2页,共3页三角形,设,由二次函数的性质得出截面面积最大时,最后由勾股定理计算即可.如图所示,设截面为四边形.截面平行于直线,截面平行于直线,又平面,故四边形为矩形,其面积为.因为,所以,所以.又,所以是等腰直角三角形.设,则,所以,当且仅当时取等号.故当截面面积最大时,,在中,由勾股定理得:.本题选A.(23-24高三下·河南·阶段练习)试卷第3页,共3页学科网(北京)股份有限公司1.在正方体中,为的中点,在棱上,且,则过且与垂直的平面截正方体所得截面的面积为()A.6B.8C.12D.16(2024·四川·一模)2.设正方体的棱长为1,与直线垂直的平面截该正方体所得的截面多边形为M.则下列结论正确的是().A.M必为三角形B.M可以是四边形C.M的周长没有最大值D.M的面积存在最大值根据线面平行的性质得出截面为矩形,由余弦定理得,设,用m表示线段长及截面面积,结合基本不等式求得截面取最值时的m值,从而得出,再根据余弦定理计算即可.如图所示,设截面为四边形.截面平行于直线,截面平行于直线,又平面,故四边形为矩形,其面积为,,.设,试卷第4页,共3页则,,,时取等号,此时.在中,由余弦定理得:,所以.选A.【题后反思】1.确定截面的主要依据有(1)平面的四个公理及推论.(2)直线和平面平行的判定和性质.(3)两个平面平行的性质.2.作截面的几种方法(1)直接法:有两点在几何体的同一个面上,连接该两点即为几何体与截面的交线,找截面实际就是找交线的过程.(2)延长线法:同一个平面有两个点,可以连线并延长至与其他平面相交找到交点.(3)平行线法:过直线与直线外一点作截面,拖直线所在的面与点所在的平面平行,可以通过过点找直线的平行线找到几何体的截面的交线.总评:截面问题的常用解题策略立体问题的解题策略,主要有代数法及几何法.其中代数法主要包括坐标法、基底法.1.坐标法.就是通过建立空间直角坐标系,将几何问题转化为坐标的代数运算.如果遇到直线,主要考虑直线的方向向量;如果遇到平面,主要考虑平面的法向量.2.基底法.基底法主要是利用平面向...