串讲04 数列【八大题型串讲PPT】-2023-2024学年高二数学上学期期末考点大串讲（苏教版2019）.pptxVIP免费

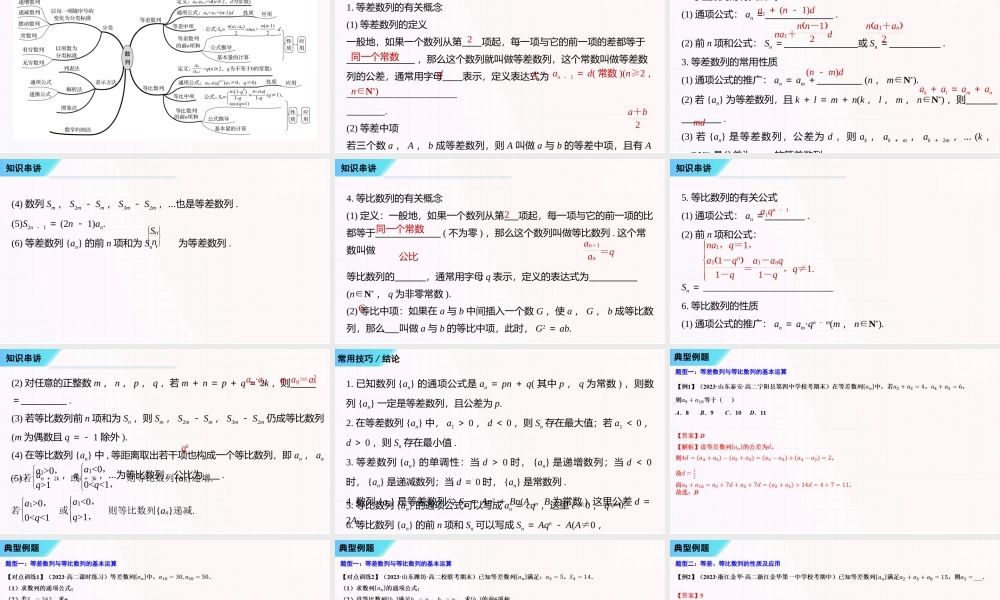
串讲04数列高二苏教版数学上册期末大串讲思维导图知识串讲常用技巧/结论典型例题思维导图知识串讲1.等差数列的有关概念(1)等差数列的定义一般地，如果一个数列从第项起，每一项与它的前一项的差都等于，那么这个数列就叫做等差数列，这个常数叫做等差数列的公差，通常用字母表示，定义表达式为_______________________.(2)等差中项若三个数a，A，b成等差数列，则A叫做a与b的等差中项，且有A2同一个常数dan－an－1＝d(常数)(n≥2，n∈N*)a＋b2知识串讲2.等差数列的有关公式(1)通项公式：an＝.(2)前n项和公式：Sn＝或Sn＝.3.等差数列的常用性质(1)通项公式的推广：an＝am＋(n，m∈N*).(2)若{an}为等差数列，且k＋l＝m＋n(k，l，m，n∈N*)，则.(3)若{an}是等差数列，公差为d，则ak，ak＋m，ak＋2m，…(k，∈N*)是公差为的等差数列a1＋(n－1)dna1＋nn－12dna1＋an2(n－m)dak＋al＝am＋anmd知识串讲(4)数列Sm，S2m－Sm，S3m－S2m，…也是等差数列.(5)S2n－1＝(2n－1)an.(6)等差数列{an}的前n项和为Sn，为等差数列.Snn知识串讲4.等比数列的有关概念(1)定义：一般地，如果一个数列从第项起，每一项与它的前一项的比都等于(不为零)，那么这个数列叫做等比数列.这个常数叫做等比数列的，通常用字母q表示，定义的表达式为(n∈N*，q为非零常数).(2)等比中项：如果在a与b中间插入一个数G，使a，G，b成等比数列，那么叫做a与b的等比中项，此时，G2＝ab.2同一个常数公比an＋1an＝qG知识串讲5.等比数列的有关公式(1)通项公式：an＝.(2)前n项和公式：Sn＝___________________________6.等比数列的性质(1)通项公式的推广：an＝am·qn－m(m，n∈N*).a1qn－1na1，q＝1，a11－qn1－q＝a1－anq1－q，q≠1.知识串讲(2)对任意的正整数m，n，p，q，若m＋n＝p＋q＝2k，则＝.(3)若等比数列前n项和为Sn，则Sm，S2m－Sm，S3m－S2m仍成等比数列(m为偶数且q＝－1除外).(4)在等比数列{an}中,等距离取出若干项也构成一个等比数列，即an，an＋k，an＋2k，an＋3k，…为等比数列，公比为.am·anap·aq＝a2kqk(5)若a1>0，q>1或a1<0，00，01，则等比数列{an}递减.常用技巧/结论1.已知数列{an}的通项公式是an＝pn＋q(其中p，q为常数)，则数列{an}一定是等差数列，且公差为p.2.在等差数列{an}中，a1＞0，d＜0，则Sn存在最大值；若a1＜0，d＞0，则Sn存在最小值...